Multiscale modelling of coupled Ca2+ channels using coloured stochastic Petri nets
- PMID: 23919953
- PMCID: PMC8687329
- DOI: 10.1049/iet-syb.2012.0017
Multiscale modelling of coupled Ca2+ channels using coloured stochastic Petri nets
Abstract
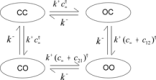
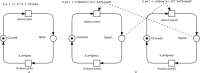
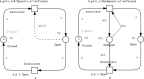
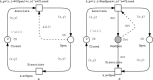
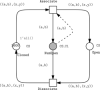
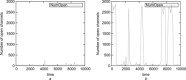
Stochastic modelling of coupled Ca2+ channels is a challenge, especially when the coupling of the channels, as determined by their spatial arrangement relative to each other, has to be considered at multiple spatial scales. In this study, the authors address this problem using coloured stochastic Petri nets (SPNc) as high-level description to generate continuous-time Markov chains. The authors develop several models with increasing complexity. They first apply SPNc to model single clusters of coupled Ca2+ channels arranged in a regular or irregular lattice, where they describe how to represent the geometrical arrangement of Ca2+ channels relative to each other using colours. They then apply this modelling idea to construct more complex models by modelling spatially arranged clusters of channels. The authors' models can be easily reproduced and adapted to different scenarios.
Figures
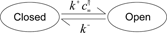

Similar articles
-
Coloured Petri nets for multilevel, multiscale and multidimensional modelling of biological systems.Brief Bioinform. 2019 May 21;20(3):877-886. doi: 10.1093/bib/bbx150. Brief Bioinform. 2019. PMID: 29112705 Free PMC article. Review.
-
Coloured Hybrid Petri Nets: An adaptable modelling approach for multi-scale biological networks.Comput Biol Chem. 2018 Oct;76:87-100. doi: 10.1016/j.compbiolchem.2018.05.023. Epub 2018 May 28. Comput Biol Chem. 2018. PMID: 29982167
-
Modelling and simulating reaction-diffusion systems using coloured Petri nets.Comput Biol Med. 2014 Oct;53:297-308. doi: 10.1016/j.compbiomed.2014.07.004. Epub 2014 Jul 15. Comput Biol Med. 2014. PMID: 25150626
-
An Exclusion Zone for Ca2+ Channels around Docked Vesicles Explains Release Control by Multiple Channels at a CNS Synapse.PLoS Comput Biol. 2015 May 7;11(5):e1004253. doi: 10.1371/journal.pcbi.1004253. eCollection 2015 May. PLoS Comput Biol. 2015. PMID: 25951120 Free PMC article.
-
Stochastic approaches for modelling in vivo reactions.Comput Biol Chem. 2004 Jul;28(3):165-78. doi: 10.1016/j.compbiolchem.2004.05.001. Comput Biol Chem. 2004. PMID: 15261147 Review.
Cited by
-
Snoopy's hybrid simulator: a tool to construct and simulate hybrid biological models.BMC Syst Biol. 2017 Jul 28;11(1):71. doi: 10.1186/s12918-017-0449-6. BMC Syst Biol. 2017. PMID: 28754122 Free PMC article.
-
Fuzzy Stochastic Petri Nets for Modeling Biological Systems with Uncertain Kinetic Parameters.PLoS One. 2016 Feb 24;11(2):e0149674. doi: 10.1371/journal.pone.0149674. eCollection 2016. PLoS One. 2016. PMID: 26910830 Free PMC article.
-
BioModelKit - An Integrative Framework for Multi-Scale Biomodel-Engineering.J Integr Bioinform. 2018 Sep 6;15(3):20180021. doi: 10.1515/jib-2018-0021. J Integr Bioinform. 2018. PMID: 30205646 Free PMC article.
-
Coloured Petri nets for multilevel, multiscale and multidimensional modelling of biological systems.Brief Bioinform. 2019 May 21;20(3):877-886. doi: 10.1093/bib/bbx150. Brief Bioinform. 2019. PMID: 29112705 Free PMC article. Review.
References
-
- Dallon J.C.: ‘Multiscale modeling of cellular systems in biology’, Curr. Opin. Coll. Interface Sci., 2010, 15, (1–2), pp. 24–31 (doi: 10.1016/j.cocis.2009.05.007) - DOI
-
- Liu F.: ‘Colored Petri nets for systems biology’. PhD thesis, Brandenburg University of Technology, Cottbus, 2012.
-
- Baldan P. Cocco N. Marin A., and Simeoni M.: ‘Petri nets for modelling metabolic pathways: a survey’, Nat. Comput., 2010, 9, (4), pp. 955–989 (doi: 10.1007/s11047-010-9180-6) - DOI
-
- Marwan W. Wagler A., and Weismantel R.: ‘Petri nets as a framework for the reconstruction and analysis of signal transduction pathways and regulatory networks’, Nat. Comput., 2011, 10, (2), pp. 639–654 (doi: 10.1007/s11047-009-9152-x) - DOI
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources
Other Literature Sources
Miscellaneous

