Cell guidance on nanogratings: a computational model of the interplay between PC12 growth cones and nanostructures

Abstract

Background: Recently, the effects of nanogratings have been investigated on PC12 with respect to cell polarity, neuronal differentiation, migration, maturation of focal adhesions and alignment of neurites.

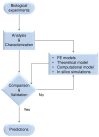
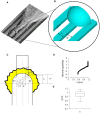
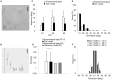
Methodology/principal findings: A synergistic procedure was used to study the mechanism of alignment of PC12 neurites with respect to the main direction of nanogratings. Finite Element simulations were used to qualitatively assess the distribution of stresses at the interface between non-spread growth cones and filopodia, and to study their dependence on filopodial length and orientation. After modelling all adhesions under non-spread growth cone and filopodial protrusions, the values of local stress maxima resulted from the length of filopodia. Since the stress was assumed to be the main triggering cause leading to the increase and stabilization of filopodia, the position of the local maxima was directly related to the orientation of neurites. An analytic closed form equation was then written to quantitatively assess the average ridge width needed to achieve a given neuritic alignment (R(2) = 0.96), and the alignment course, when the ridge depth varied (R(2) = 0.97). A computational framework was implemented within an improved free Java environment (CX3D) and in silico simulations were carried out to reproduce and predict biological experiments. No significant differences were found between biological experiments and in silico simulations (alignment, p = 0.3571; tortuosity, p = 0.2236) with a standard level of confidence (95%).

Conclusions/significance: A mechanism involved in filopodial sensing of nanogratings is proposed and modelled through a synergistic use of FE models, theoretical equations and in silico simulations. This approach shows the importance of the neuritic terminal geometry, and the key role of the distribution of the adhesion constraints for the cell/substrate coupling process. Finally, the effects of the geometry of nanogratings were explicitly considered in cell/surface interactions thanks to the analytic framework presented in this work.

Figure 1. Regenerative interface (External and internal views).

(A) Scheme of reciprocal positions of (1) Healthy stump of nerve; (2) Regenerative scaffold; (3) Contacts with active sites. The healthy stump of nerve is connected with the regenerative scaffold to allow the injured axons to regenerate and contact the active sites. From these contacts, electrical signals, closely related to the patient’s will of movement, can be achieved to drive neural prostheses. (B) Internal view of regenerative scaffold with active topographic constraints (e.g. nanogratings). This kind of structure could be able to split the beam of axons improving the selectivity of contacts with the active sites. Two different populations of axons (e.g. sensory and motor) are shown in red and blue. In this concept, the beam of axon was split by the synergy of nanotopography and chemical cues.

Figure 2. Logic flow of activities.

Scheme of the activities carried out in this study: images of outgrowing neurites were taken from biological experiments performed on PC12, and analysed to investigate the morphology of terminals. Simple FE models were built from these morphological data to study, accounting for geometry and constraints, the course of stress at the intersection between collapsed growth cones and filopodia. Then, an analytic model was written to account for the nanograting geometry and to implement in silico simulations. In silico results were compared with biological data to validate the whole procedure and to provide predictions on more complex geometries.

Figure 3. From biological experiments to computational models.

(A) A SEM image of filopodia emerging from a non-spread growth cone (bar = 1 µm). (B) FE model of a non-spread growth cone showing a simplified geometry together with an emerging filopodium. The set of parameters necessary to characterize the nanograting geometry is also shown: ridge width r_w, groove width g_w, and ridge depth r_d. (C) Bidimensional model of interactions between non-spread growth cone and ridge surface. Point K2 (together with K1, symmetric with respect to the centreline of the filopodial shaft) shows the limit angle β_lim. The quantity h^* was connected to the actual intersection angle through a fraction of the ridge width (a). (D,E) Quantile-quantile plot of the quantity h as derived from in silico simulations, together with its box plot.

Figure 4. Analysis of neuritic terminals.

(A) Typical bright field images of PC12 cells differentiated by NGF on period 1, 1.5 and 2 gratings and on flat substrate (from the top, respectively). White arrows: grating direction; bars = 20 µm. (B) Typical confocal images of the morphological aspect of terminals with non-spread growth cones: PC12 neurite terminals grown on period 1, 1.5 and 2 gratings and on flat substrate, and stained for β3-Tubulin (green) and actin (red). Each panel side = 25 µm; square inset: grating direction. (C) Analysis of PC12 neuritic terminals over different nanogratings (periods 1, 1.5, 2 µm) and flat substrate: terminals were characterized with respect to their morphology as spread or non-spread growth cones. The analysis was carried out on 323 terminals. (D) SEM images of PC12 growth cones on period 1 nanogratings: a spread growth cone (left), magnification = 3110 X, bar length =  1 µm; a non-spread growth cone, presenting lateral transient processes (right), magnification = 12550 X, bar length =  1 µm.

Figure 5. Finite Element models of non-spread growth cones.

(A) Displacement field for FE models of a non-spread growth cone with three (up) and one (down) emerging filopodium. The displacements were normalized over the global maximum over the whole non-spread growth cone, which accounted for the contraction of the neuritic cytoskeleton. The distribution of displacement was linear and similar among different filopodia (up). It was also similar to the displacement distribution of the model with one emerging filopodium (down). (B) Von Mises stress field for FE models of a non-spread growth cone with three (up) and one (down) emerging filopodium. VM stresses were normalized over the maximum stress at the tip of the shortest filopodium. Unlike the displacement field, the VM stresses varied among filopodia of different lengths. In particular, the course of VM along the shortest filopodium was similar for both models with three and one emerging protrusion. Arrows pointed the investigated local maxima of VM stress at the intersection between non-spread growth cones and filopodia for both models (up and down).(C) Vector plots of principal stresses for both models; left: magnification of the vector field for the model with three emerging filopodia; right: magnification of the vector field for the model with one emerging filopodium. In this case also, both fields were similar but scaled. (D) Modular surfaces accounting for the variation of intersection VM stress with filopodial orientation and length. The plot accounted for angular variation in the range (−10°, 10°) and different length of filopodia in the range 0.001–2 where was the radius of the non-spread growth cone. All values were normalized on the interface VM stress at 0° for a length of 0.001 _.

Figure 6. Analytic model.

(A) Quantitative prediction of the ridge width to achieve a given mean alignment angle β. All experimental points were obtained keeping the ridge depth constant (350 nm) while the ridge width varied in the range 500–2000 nm. Inset: magnification for small values of β. (B) Influence of the ridge depth on the value of β when the ridge width was kept constant and the ridge depth varied between 0 (flat) and 350 nm.

Figure 7. In silico predictions of biological experiments.

(A) DIC image of a cell culture acquired with an inverted Nikon-Ti PSF wide field microscope: PC12 cells were differentiated on a nanograting with period 1 and the black arrow shows the main direction of the grating. (B) Biological experiment (see A) simulated in CX3D. In silico cells were placed on a virtual nanograting with the same geometry of biological experiments and neurites grew according to the framework described by Eqs. (1–4). The black arrow indicates the main direction of the grating. (C) Comparison between biological and in silico alignments. Biological data were collected at t = 12, 36, 60 h, while in silico values were kept at t = 6, 12, 18, 24, 30, 36, 42, 48, 54, 60 h (61 neurites, error bars = standard deviations). Then, the mean biological and in silico values were compared and a Welch t-test resulted in p =  0.3571 (no significant difference). (D) Comparison between experimental, theoretical and in silico mean tortuosity (117 neurites). No significant difference was found in PC12 between experimental and in silico values of tortuosity (Wilcoxon rank sum test, p = 0.2236). (E) Control of neuritic orientation for neurites on a period 1 nanograting in biological experiments and in silico simulations. The percentages of neurites aligned to the grating axis within different angular ranges were reported: in both cases, most of the neurites aligned within 20° with respect to the main grating direction. The range of orientations was similar in both cases. (F) Temporal evolution of orientation control for neurites in CX3D physical space. The orientation of neurites was reported at t = 12, 36 and 60 h and showed small differences over time. Most neurites aligned to the main grating direction within small angular ranges (±20°) for any sampled time.

Figure 8. In silico simulations of beam splitting experiments.

(A) In silico simulation of a group of 30 cells on a swallowtail grating. Different phases of neuritic outgrowth are shown on the planes (in perspective) over time (t). In simulations, geometric and fasciculation effects were considered together. (B) Geometrical angles to model the swallowtail: the φ angle accounted for the steepness of the change between the straight grating and the following bifurcation. (C) Percentage of turning axons with different values of the φ (swallowtail) angle. This percentage decreased as the φ angle increased, in agreement with literature .