Equilibria of an epidemic game with piecewise linear social distancing cost
- PMID: 23943363
- PMCID: PMC6690478
- DOI: 10.1007/s11538-013-9879-5
Equilibria of an epidemic game with piecewise linear social distancing cost
Abstract
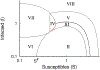
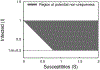
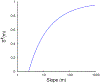
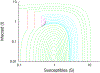
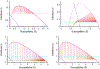
Around the world, infectious disease epidemics continue to threaten people's health. When epidemics strike, we often respond by changing our behaviors to reduce our risk of infection. This response is sometimes called "social distancing." Since behavior changes can be costly, we would like to know the optimal social distancing behavior. But the benefits of changes in behavior depend on the course of the epidemic, which itself depends on our behaviors. Differential population game theory provides a method for resolving this circular dependence. Here, I present the analysis of a special case of the differential SIR epidemic population game with social distancing when the relative infection rate is linear, but bounded below by zero. Equilibrium solutions are constructed in closed-form for an open-ended epidemic. Constructions are also provided for epidemics that are stopped by the deployment of a vaccination that becomes available a fixed-time after the start of the epidemic. This can be used to anticipate a window of opportunity during which mass vaccination can significantly reduce the cost of an epidemic.
Figures
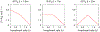




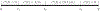
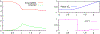


References
-
- Arrow KJ and Kurz M (1970). Public Investment, the Rate of Return, and Optimal Fiscal Policy. Baltimore, MD: Johns Hopkins Press.
-
- Auld M (2003). Choices, beliefs, and infectious disease dynamics. Journal of Health Economics 22, 361–377. - PubMed
-
- Bressan A and Piccoli B (2007). Introduction to the Mathematical Theory of Control. American Institute of Mathematical Sciences.
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Medical

