Toward a comprehensive framework for the spatiotemporal statistical analysis of longitudinal shape data
- PMID: 23956495
- PMCID: PMC3744347
- DOI: 10.1007/s11263-012-0592-x
Toward a comprehensive framework for the spatiotemporal statistical analysis of longitudinal shape data
Abstract
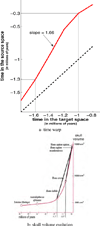
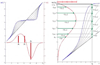
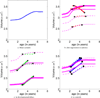
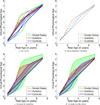
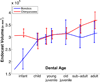
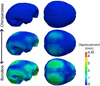
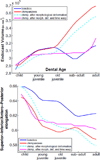
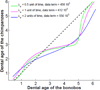
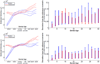
This paper proposes an original approach for the statistical analysis of longitudinal shape data. The proposed method allows the characterization of typical growth patterns and subject-specific shape changes in repeated time-series observations of several subjects. This can be seen as the extension of usual longitudinal statistics of scalar measurements to high-dimensional shape or image data. The method is based on the estimation of continuous subject-specific growth trajectories and the comparison of such temporal shape changes across subjects. Differences between growth trajectories are decomposed into morphological deformations, which account for shape changes independent of the time, and time warps, which account for different rates of shape changes over time. Given a longitudinal shape data set, we estimate a mean growth scenario representative of the population, and the variations of this scenario both in terms of shape changes and in terms of change in growth speed. Then, intrinsic statistics are derived in the space of spatiotemporal deformations, which characterize the typical variations in shape and in growth speed within the studied population. They can be used to detect systematic developmental delays across subjects. In the context of neuroscience, we apply this method to analyze the differences in the growth of the hippocampus in children diagnosed with autism, developmental delays and in controls. Result suggest that group differences may be better characterized by a different speed of maturation rather than shape differences at a given age. In the context of anthropology, we assess the differences in the typical growth of the endocranium between chimpanzees and bonobos. We take advantage of this study to show the robustness of the method with respect to change of parameters and perturbation of the age estimates.
Keywords: growth; longitudinal data; shape regression; spatiotemporal registration; statistics; time warp.
Figures







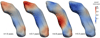




References
-
- Aljabar P, Bhatia K, Murgasova M, Hajnal J, Boardman J, Srinivasan L, Rutherford M, Dyet L, Edwards A, Rueckert D. Assessment of brain growth in early childhood using deformation-based morphometry. NeuroImage. 2008;39(1):348–358. - PubMed
-
- Allassonnière S, Kuhn E. Stochastic algorithm for bayesian mixture effect template estimation. ESAIM Probability and Statistics. 2009 In Press.
-
- Chandrashekara R, Rao A, Sanchez-Ortiz G, Mohiaddin RH, Rueckert D. Construction of a statistical model for cardiac motion analysis using nonrigid image registration. Information Processing in Medical Imaging, Springer, Lecture Notes in Computer Science. 2003;vol 2732:599–610. - PubMed
-
- de Craene M, Camara O, Bijnens BH, Frangi AF. Large diffeomorphic FFD registration for motion and strain quantification from 3D-US sequences. Proc. of Functional Imaging and Modeling of the Heart, Spinger, LNCS. 2009;vol 5528:437–446.
Grants and funding
LinkOut - more resources
Full Text Sources
