Dose verification in intensity modulation radiation therapy: a fractal dimension characteristics study

Abstract

Purpose: This study describes how to identify the coincidence of desired planning isodose curves with film experimental results by using a mathematical fractal dimension characteristic method to avoid the errors caused by visual inspection in the intensity modulation radiation therapy (IMRT).

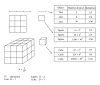
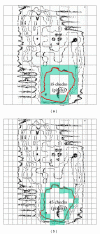
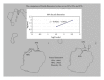
Methods and materials: The isodose curves of the films delivered by linear accelerator according to Plato treatment planning system were acquired using Osiris software to aim directly at a single interested dose curve for fractal characteristic analysis. The results were compared with the corresponding planning desired isodose curves for fractal dimension analysis in order to determine the acceptable confidence level between the planning and the measurement.

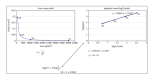
Results: The film measured isodose curves and computer planning curves were deemed identical in dose distribution if their fractal dimensions are within some criteria which suggested that the fractal dimension is a unique fingerprint of a curve in checking the planning and film measurement results. The dose measured results of the film were presumed to be the same if their fractal dimension was within 1%.

Conclusions: This quantitative rather than qualitative comparison done by fractal dimension numerical analysis helps to decrease the quality assurance errors in IMRT dosimetry verification.

Figure 1

This figure illustrates the understanding and meaning of the power law behavior in a pure mathematical situation in Koch Island. Each Koch curve can be divided into four self-similar parts, which are similar to the entire curve via a similarity transformation which in turn is similar to the entire curve of Figure 3.

Figure 2

The relationship between the reduction factor (scaling factor) and the number of scaleddown pieces into which the structure is divided. Apparently, for the line, square, and cube, there is a nice power law relationship between the numbers of pieces, a, and the reduction factors. This law is a = 1/S ^D where D = 1 for the line, D = 2 for the square, and D = 3 for the cube.

Figure 3

This figure shows how the dose curve is adopted for fractal analysis. The original resolution (left on the figure) is 486 pixels × 711 pixels with 8 bits/pixel. The scale is then reduced by 1/2, 1/4, and 1/8 (from right up to right bottom) to give 243 × 356, 122 × 178, and 61 × 89 pixels to measure the length of the same isodose curve adopted in the film. The planning dose curve Ds is then compared to that of planning result. The curve of low resolution (lower right) is coarse and big while high resolution (upper right) shows slim curves.

Figure 4

The law seems to be relevant of scale verse tarea on left hand side in this figure, which is a power law of the form y ∝ x ^d (where y denotes the length, x denote the scale, and d is the dimension). Take the logarithm of the length of each region of interest and logarithm (1/scale), and then plot log⁡⁡(length) against log⁡⁡(1/scale); then the slope is in the form y = ax + b. The slope can represent the unique characteristics of the curve.

Figure 5

When these two dose distributions are normalized at their cross hair isocenter, the 88% region of the interested planning isodose curve's Ds is 1.9852, and the 88% region of the interested film isodose curve's Ds is 1.9841. The discrepancy is only 5 × 10⁻⁴[(1.9852 − 1.9841)/1.9852]. The planning 88% isodose curve and film 88% isodose curve are supposed to be identical if the difference between their Ds values is within 1%.

Figure 6

The relationship between length and scale (tiles size) can be implemented by transforming an image into a mosaic and regarding the elements (individual tiles) of the mosaic as being square tiles laid around the boundary. The mosaic transformation can be used to set up a procedure for evaluating the fractal structure of the boundary by a technique known as mosaic amalgamation. The perimeter estimated in (a) is smaller than (b) due to the larger scale (the length of the mosaic tile) used in (a).

Figure 7

In this figure, the selected 85% is interesting to study. The fractal dimension magnitude criterion of acceptability between the desired planning curves and the delivered dose curves can be made by descending or increasing the isodose curves from 85% downwards or upwards to see which isodose curve is still regarded as one fractal value. When the fractal dimensions, 83% and 87%, are compared to 85% curve, the variation of fractal dimension is within 1%, which means that the two curves are identical only if their fractal dimension is within 1%.