Statistical mechanical treatments of protein amyloid formation

Abstract

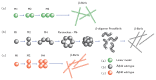
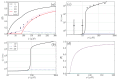
Protein aggregation is an important field of investigation because it is closely related to the problem of neurodegenerative diseases, to the development of biomaterials, and to the growth of cellular structures such as cyto-skeleton. Self-aggregation of protein amyloids, for example, is a complicated process involving many species and levels of structures. This complexity, however, can be dealt with using statistical mechanical tools, such as free energies, partition functions, and transfer matrices. In this article, we review general strategies for studying protein aggregation using statistical mechanical approaches and show that canonical and grand canonical ensembles can be used in such approaches. The grand canonical approach is particularly convenient since competing pathways of assembly and dis-assembly can be considered simultaneously. Another advantage of using statistical mechanics is that numerically exact solutions can be obtained for all of the thermodynamic properties of fibrils, such as the amount of fibrils formed, as a function of initial protein concentration. Furthermore, statistical mechanics models can be used to fit experimental data when they are available for comparison.

Figure 1

(a) A linear model for aggregation where M-mers grow one monomer at a time in a one-dimensional fashion; (b) A model for Aβ (1-42) wild-type proteins aggregating into fibrils. Monomers assemble until reaching a critical concentration, for example, a hexamer, as illustrated. Hexamers then aggregate into more complex structures such as protofibrils, and eventually full fibrils; and (c) a model for Aβ(1-40) wild-type protein aggregation where monomers join to form dimers, which may grow into protofibrils and eventually fibrils.

Figure 2

In both (a) and (b), the illustrated cross-β structure is the sequence segment GNNQQNY from the prion Sup35. Carbon atoms are purple or grey/white, oxygen atoms are red, and nitrogen atoms are blue. In (a), cross-β structure is illustrated. Grey arrows represent the back-bone of a β-strand, and the side-chains are shown projecting from the strands. Purple arrows represent the strands residing in the back of the structure. The regions between the strands are referred to as the dry interfaces, whereas just outside of strands are wet interfaces. The fibril axis is indicated by an arrow running through the dry regions between the strands; (b) Side view of the fibril. The H-bonds are formed between red carboxyl groups and blue amide groups from adjacent layers; in (c), a top view of the fibrils shows the interdigitation of two β-sheets, referred to as the steric zipper. Within the steric zipper, water molecules are absent (a red plus sign indicates water). Both images are reprinted from Nelson et al. [48,49].

Figure 3

Cartoon illustrations of an Aβ protofibril are shown. Left: Looking down the axis of the fibril (z-axis); Right: A sideview of the protofibril illustrating the twisted, helical pattern. Proteins are spaced at ≈5 Å, and the chiral twist of 0.833 degree/°A was arbitrarily chosen for illustrative purposes. Image reprinted from Petkova et al. [50].

Figure 4

A ZB model for protein aggregation is illustrated, where the proteins (circles) in aggregates can be coil (white), sheet (black), or helix (red marked with X) in conformation. The free energies associated with each conformation are listed, as well as the interfacial free energies R₁, R₂, and R₃ between helix-coil, sheet-coil, or helix-sheet regions, respectively.

Figure 5

(a) Front-view (y-z plane) of a strip lattice representing an aggregate of Aβ(1–40) proteins. Black circles corresponds to coil proteins while white circles denote sheet or helix proteins. Dashed lines represent interactions between proteins in the y-direction whereas solid lines are the interactions between proteins along the x-axis; (b) Side-view (x-y plane) of Aβ-40 proteins illustrating the steric zipper; and (c) strip lattice representation of the Aβ-40proteins, where the parameters B and K are illustrated.

Figure 6

(a) Lattice representation and transfer matrix of α-synuclein fibrils composed of 4 filaments; (b) The fibril for Aβ is composed of two protofibrils, each represented by a strip lattice and spin-variables s and t. The strips are stacked in-register along the z-axis, and the parameter B (dashed, green) lines represents the bonds between sheet proteins in protofibrils or fibrils.

Figure 7

(a) A strip lattice with periodic boundary conditions in the y-axis is used to model the nucleus for Aβ(1–42) as a hexamer. The strip has L_y monomers per column in general. B (blue, dotted lines) is the free energy contribution from the interaction between proteins $s_i^j,\hspace{0.17em}{s}_i^{j+1}$ that are both sheet along the y-axis; (b) Oligomers aggregate along the x-axis with a total of L_x sites, where L_x → ∞ is the thermodynamic limit.

Figure 8

Partial lists of chemical species that may exist in dynamic equilibrium with fibrils for Aβ(1–40) (top) and α-synuclein (bottom). In the Aβ model, the different types of aggregates that could be present at equilibrium are 1D filaments, strips of length L_y = 2 that represent protofibrils, and 3D cubes that represent fibrils. The cubes are composed of two identical proto-fibrils stacked in-register. In the model for α-synuclein aggregates, L_y = 1, 2, 3, and 4 strip lattices are used to describe the aggregates at equilibrium, with the L_y = 4 strip lattice representing the fibril. For both Aβ(1–40) and α-synuclein, we assumed n_c = 2.

Figure 9

(a) Plot of 〈θ₂〉 for 1D, 2D, and 3D structures in the Aβ(1–40) model. Black dots represent the CD data from Terzi, et al. [52], where we the total fraction of sheet proteins in aggregates of any species; (b) Predicted average lengths, 〈L〉, of the Aβ(1–40) fibrils using the fit parameters found in (a); In plot (c), the AFM data for the α-synuclein fibrils is plotted as black dots, along with the fit function 〈L〉 [68]. We fit 〈L〉 using the L_y = 4 strip lattice model; In (d), 〈θ₂〉 for α-synuclein (solid, purple curve) is compared with ρ_fib/φ (dashed, black curve) by using the fit parameters found in (c); In (a) and (b), the fit parameters for the Aβ(1–40) model were: P₁ = 7.41RT, B = 1.4RT, R₂ = −2.47RT, and K = 0.45RT. In (a), η = 1 − (z + z² + z⁴)/φ; In (c) and (d), the fit parameters for the α-synuclein model were P₁ = K = 2.7RT, B = 1.95RT and R₂ = −1.64RT.

Figure 10

Summary of protein conformation energies. A site could be occupied with a solvent cluster, denoted by n = 0 (square), or a protein, n = 1 (circles). Proteins may assume a particular conformation (sheet, black/solid circle; coil, white circle). A dilute q = 2 Potts model for sheet-coil conformations is shown, where n_c = 1 and the free energies P₁, K, R, and A are illustrated.

Figure 11

Proteins or solvent clusters may occupy lattice sites, where the front-view (y–z plane) of an aggregate of Aβ(1–40) proteins is shown along with the interactions between proteins and solvent clusters. The n_c = 2 nucleus is represented by dashed-dotted lines (free energy A denoting the nucleation). Dotted and solid lines illustrate interactions between sheet proteins. Double solid lines illustrate a protein-solvent interface. Dashed (blue) lines have no meaning.

Figure 12

(a) 〈θ〉/〈N_p〉 is fitted to the results of the Terzi et al. experiment [52] involving Aβ(1–40) aggregates; (b) The fraction of sheet proteins in Curli fibrils is fitted to the scaled results of the Hammer et al. experiment [84]. In (a), the fit parameters were P₁ ≈ K ≈ A ≈ 0 kcal/mol, R₁ = 0.35 kcal/mol, and F = 16.4 kcal/mol.; while in (b) we have P₁ = 7.26 kcal/mol, K = 2.2 kcal/mol, R₁ ≈ 0 kcal/mol, and A = 1.2 kcal/mol [26]. In (a) we used case B of the strip models with n_c = 2 whereas in (b) we used the 1D model with n_c = 2 for aggregation. In both cases q = 2.