Bayesian hierarchical modeling of patient subpopulations: efficient designs of Phase II oncology clinical trials

Abstract

Background: In oncology, the treatment paradigm is shifting toward personalized medicine, where the goal is to match patients to the treatments most likely to deliver benefit. Treatment effects in various subpopulations may provide some information about treatment effects in other subpopulations.

Purpose: We compare different approaches to Phase II trial design where a new treatment is being investigated in several groups of patients. We compare considering each group in an independent trial to a single trial with hierarchical modeling of the patient groups.

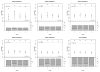
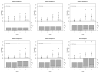
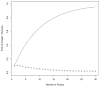
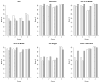
Methods: We assume four patient groups with different background response rates and simulate operating characteristics of three trial designs, Simon's Optimal Two-Stage design, a Bayesian adaptive design with frequent interim analyses, and a Bayesian adaptive design with frequent interim analyses and hierarchical modeling across patient groups.

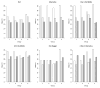
Results: Simon's designs are based on 10% Type I and Type II error rates. The independent Bayesian designs are tuned to have similar error rates, but may have a slightly smaller mean sample size due to more frequent interim analyses. Under the null, the mean sample size is 2-4 patients smaller. A hierarchical model across patient groups can provide additional power and a further reduction in mean sample size. Under the null, the addition of the hierarchical model decreases the mean sample size an additional 4-7 patients in each group. Under the alternative hypothesis, power is increased to at least 98% in all groups.

Limitations: Hierarchical borrowing can make finding a single group in which the treatment is promising, if there is only one, more difficult. In a scenario where the treatment is uninteresting in all but one group, power for that one group is reduced to 65%. When the drug appears promising in some groups and not in others, there is potential for borrowing to inflate the Type I error rate.

Conclusions: The Bayesian hierarchical design is more likely to correctly conclude efficacy or futility than the other two designs in many scenarios. The Bayesian hierarchical design is a strong design for addressing possibly differential effects in different groups.

Figure 1

Example 1. Barplot shows sample size in each group where the height of the solid bar shows number of patients enrolled and height of the hashed bar shows number of patients who achieved a response. Upper part of the plot shows observed response (‘x’), fitted response (‘o’) and 2 times the standard deviation (line). Asterisks indicate Pr(p > pmid) for the interim analyses and Pr(p > p₀) at the final analysis.

Figure 2

Example 2. Barplot shows sample size in each group where the height of the solid bar shows number of patients enrolled and height of the hashed bar shows number of patients who achieved a response. Upper part of the plot shows observed response (‘x’), fitted response (‘o’) and 2 times the standard deviation (line). Asterisks indicate Pr(p > pmid) for the interim analyses and Pr(p > p₀) at the final analysis.

Figure 3

Probability of claiming efficacy by group in each scenario. The open bar is Simon’s design, the crosshatched bar is independent Bayesian, and the solid bar is Bayesian hierarchical.

Figure 4

Overall Type I error rate, probability of claiming efficacy in at least one group under the null hypothesis by the number of groups. Simon’s design is shown as a solid line and the Bayesian hierarchical design is shown as the dotted line. We assume p₀ = 10% and p₁ = 30% for all groups.

Figure 5

Mean sample size by group in each scenario. The open bar is Simon’s design, the crosshatched bar is independent Bayesian, and solid bar is Bayesian hierarchical.

Figure 6

Mean sample size by group in each scenario with early efficacy stopping for the two Bayesian designs. The open bar is Simon’s design, the crosshatched bar is independent Bayesian, and solid bar is Bayesian hierarchical.