Pooling of first-order inputs in second-order vision
- PMID: 23994031
- PMCID: PMC3815703
- DOI: 10.1016/j.visres.2013.08.005
Pooling of first-order inputs in second-order vision
Abstract
The processing of texture patterns has been characterized by a model that first filters the image to isolate one texture component, then applies a rectifying nonlinearity that converts texture variation into intensity variation, and finally processes the resulting pattern with mechanisms similar to those used in processing luminance-defined images (spatial-frequency- and orientation-tuned filters). This model, known as FRF for filter rectify filter, has the appeal of explaining sensitivity to second-order patterns in terms of mechanisms known to exist for processing first-order patterns. This model implies an unexpected interaction between the first and second stages of filtering; if the first-stage filter consists of narrowband mechanisms tuned to detect the carrier texture, then sensitivity to high-frequency texture modulations should be much lower than is observed in humans. We propose that the human visual system must pool over first-order channels tuned to a wide range of spatial frequencies and orientations to achieve texture demodulation, and provide psychophysical evidence for pooling in a cross-carrier adaptation experiment and in an experiment that measures modulation contrast sensitivity at very low first-order contrast.
Keywords: Second-order vision; Texture.
Copyright © 2013 Elsevier Ltd. All rights reserved.
Figures


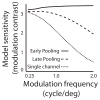









References
-
- Barlow HB, Kaushal TP, Hawken M, Parker AJ. Human contrast discrimination and the threshold of cortical neurons. Journal of the Optical Society of America A. 1987;4:2366– 2371. - PubMed
-
- Bergen JR, Landy MS. Computational modeling of visual texture segregation. In: Landy MS, Movshon AJ, editors. Computational Models of Visual Processing. Cambridge, Mass: MIT Press; 1991. pp. 253–271.
-
- Dakin SC, Mareschal I. Sensitivity to contrast modulation depends on carrier spatial frequency and orientation. Vision Research. 2000;40:311–329. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

