Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2013 Jul 1:63:63-80.
doi: 10.1016/j.csda.2013.01.023.

RECENT PROGRESS IN THE NONPARAMETRIC ESTIMATION OF MONOTONE CURVES -WITH APPLICATIONS TO BIOASSAY AND ENVIRONMENTAL RISK ASSESSMENT

Rabi Bhattacharya  1 , Lizhen Lin
Affiliations

RECENT PROGRESS IN THE NONPARAMETRIC ESTIMATION OF MONOTONE CURVES -WITH APPLICATIONS TO BIOASSAY AND ENVIRONMENTAL RISK ASSESSMENT

Rabi Bhattacharya et al. Comput Stat Data Anal. .

Abstract

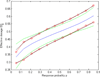
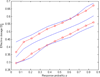
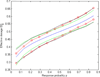
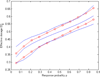
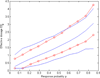
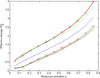
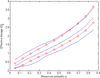
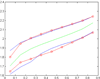
Three recent nonparametric methodologies for estimating a monotone regression function F and its inverse F-1 are (1) the inverse kernel method DNP (Dette et al. (2005), Dette and Scheder (2010)), (2) the monotone spline (Kong and Eubank (2006)) and (3) the data adaptive method NAM (Bhattacharya and Lin (2010), (2011)), with roots in isotonic regression (Ayer et al. (1955), Bhattacharya and Kong (2007)). All three have asymptotically optimal error rates. In this article their finite sample performances are compared using extensive simulation from diverse models of interest, and by analysis of real data. Let there be m distinct values of the independent variable x among N observations y. The results show that if m is relatively small compared to N then generally the NAM performs best, while the DNP outperforms the other methods when m is O(N) unless there is a substantial clustering of the values of the independent variable x.

PubMed Disclaimer

Figures

Figure 1
Figure 1. [Probit]
[Probit Data]95% CI for NAM, DNP and MLE (m=5,n=5).
Figure 2
Figure 2. [Probit]
[Probit Data]95% CI for NAM, DNP and MLE (m=5,n=10).
Figure 3
Figure 3. [Probit]
[Probit Data]95% CI for NAM and SP (m=5,n=10).
Figure 4
Figure 4. [Probit]
[Probit Data]95% CI for NAM, DNP and MLE (m=5,n=25).
Figure 5
Figure 5. [Probit]
[Probit Data]95% CI for NAM and SP (m=5,n=25).
Figure 6
Figure 6. [Weibull]
[Weibull Data]95% CI for NAM, DNP, SP and MLE (m=10,n=5).
Figure 7
Figure 7. [Weibull]
[Weibull Data]95% CI for NAM and SP (m=10,n=5).
Figure 8
Figure 8. [Weibull]
[Weibull Data]95% CI for NAM, DNP, SP and MLE (m=10,n=10).
Figure 9
Figure 9. [Weibull]
[Weibull Data]95% CI for NAM and SP (m=10,n=10).
Figure 10
Figure 10. [Weibull]
[Weibull Data]95% CI for NAM, DNP, SP and MLE (m=10,n=25).
Figure 11
Figure 11. [Weibull]
[Weibull Data]95% CI for NAM and SP (m=10,n=25).
Figure 12
Figure 12. [Logit]
[Logistic Data]95% CI for m=10, n=5 for Smoothing curve and NAM curve(r=3).
Figure 13
Figure 13. [Logit]
[Logistic Data]95% CI for m=10, n=10 for Smoothing curve and NAM curve(r=3).
Figure 14
Figure 14. [Logit]
[Logistic Data]95% CI for m=10, n=25 for Smoothing curve and NAM curve(r=3).
See this image and copyright information in PMC

References

    1. Ayer M, Brunk HD, Ewing GM, Reid WT, Silverman E. An empirical distribution function for sampling with incomplete information. Ann.Math.Statist. 1955;26:641–647.
    1. Bhattacharya R, Kong M. Consistency and asymptotic normality of the estimated effective dose in bioassay. J. Statist. Plan. Inf. 2007;137:643–658.
    1. Bhattacharya R, Lin L. An adaptive nonparametric method in benchmark analysis for bioassay and environmental studies. Statist. Probab. Letters. 2010;80:1947–1953. - PMC - PubMed
    1. Bhattacharya R, Lin L. Nonparametric benchmark analysis in risk assessment: a comparative study by simulation and data analysis. Sankhya, The Indian Journal of Statistics Ser.B. 2011;73(Issue 1):144–163. (2011). - PMC - PubMed
    1. Dette H, Scheder R. A finite sample comparison of nonparametric estimates of the effective dose in quantal bioassay. J. Statist. Comput. Simulation. 2010;80(5):527–544.

LinkOut - more resources