Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2014 Feb 10;33(3):517-35.
doi: 10.1002/sim.5941. Epub 2013 Aug 23.

Graphical assessment of internal and external calibration of logistic regression models by using loess smoothers

Peter C Austin  1 , Ewout W Steyerberg
Affiliations

Graphical assessment of internal and external calibration of logistic regression models by using loess smoothers

Peter C Austin et al. Stat Med. .

Abstract

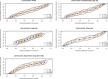
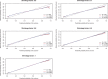
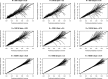
Predicting the probability of the occurrence of a binary outcome or condition is important in biomedical research. While assessing discrimination is an essential issue in developing and validating binary prediction models, less attention has been paid to methods for assessing model calibration. Calibration refers to the degree of agreement between observed and predicted probabilities and is often assessed by testing for lack-of-fit. The objective of our study was to examine the ability of graphical methods to assess the calibration of logistic regression models. We examined lack of internal calibration, which was related to misspecification of the logistic regression model, and external calibration, which was related to an overfit model or to shrinkage of the linear predictor. We conducted an extensive set of Monte Carlo simulations with a locally weighted least squares regression smoother (i.e., the loess algorithm) to examine the ability of graphical methods to assess model calibration. We found that loess-based methods were able to provide evidence of moderate departures from linearity and indicate omission of a moderately strong interaction. Misspecification of the link function was harder to detect. Visual patterns were clearer with higher sample sizes, higher incidence of the outcome, or higher discrimination. Loess-based methods were also able to identify the lack of calibration in external validation samples when an overfit regression model had been used. In conclusion, loess-based smoothing methods are adequate tools to graphically assess calibration and merit wider application.

Keywords: calibration; graphical methods; logistic regression; prediction; prediction models.

PubMed Disclaimer

Figures

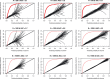
Figure 1
Figure 1
Effect of area under the receiver operating characteristic curve (AUC) and sample size on assessment of calibration.
Figure 2
Figure 2
Effect of outcome prevalence and sample size on the assessment of calibration.
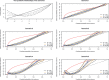
Figure 3
Figure 3
Quadratic relationship.
Figure 4
Figure 4
Quadratic relationship.
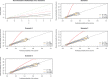
Figure 5
Figure 5
Interaction relationship: omitted binary variable and interaction term.
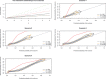
Figure 6
Figure 6
Interaction relationship: omitted interaction term.
Figure 7
Figure 7
Interaction relationship: omitted binary variable and interaction term.
Figure 8
Figure 8
Interaction relationship: omitted interaction term.
Figure 9
Figure 9
Different link functions.
Figure 10
Figure 10
Different link functions.
Figure 11
Figure 11
Shrunken linear predictor in validation sample.
Figure 12
Figure 12
Calibration of overfit prediction model in derivation/validation samples.
Figure A.1
Figure A.1
Effect of span parameter and sample size on the assessment of calibration (loess function).
Figure A.2
Figure A.2
Effect of span parameter and sample size on the assessment of calibration (lowess function)
See this image and copyright information in PMC

Comment in

References

    1. Breiman L. Random forests. Machine Learning 2001; 45(1):5–32.
    1. Hastie T, Tibshirani R, Friedman J. The Elements of Statistical Learning. Data Mining, Inference, and Prediction. Springer‐Verlag: New York, NY, 2001.
    1. Austin PC, Lee DS, Steyerberg EW, Tu JV. Regression trees for predicting mortality in patients with cardiovascular disease: what improvement is achieved by using ensemble‐based methods? Biometrical Journal 2012; 54(5):657–673. DOI: 10.1002/bimj.201100251. - DOI - PMC - PubMed
    1. Friedman J, Hastie T, Tibshirani R. Additive logistic regression: a statistical view of boosting (with discussion). The Annals of Statistics 2000; 28: 337–407.
    1. Austin PC, Tu JV, Ho JE, Levy D, Lee DS. Using methods from the data‐mining and machine‐learning literature for disease classification and prediction: a case study examining classification of heart failure subtypes. Journal of Clinical Epidemiology 2013; 66(4):398–407. - PMC - PubMed

Publication types