Effects of knots on protein folding properties
- PMID: 24023962
- PMCID: PMC3762781
- DOI: 10.1371/journal.pone.0074755
Effects of knots on protein folding properties
Abstract
This work explores the impact of knots, knot depth and motif of the threading terminus in protein folding properties (kinetics, thermodynamics and mechanism) via extensive Monte Carlo simulations of lattice models. A knotted backbone has no effect on protein thermodynamic stability but it may affect key aspects of folding kinetics. In this regard, we found clear evidence for a functional advantage of knots: knots enhance kinetic stability because a knotted protein unfolds at a distinctively slower rate than its unknotted counterpart. However, an increase in knot deepness does not necessarily lead to more effective changes in folding properties. In this regard, a terminus with a non-trivial conformation (e.g. hairpin) can have a more dramatic effect in enhancing kinetic stability than knot depth. Nevertheless, our results suggest that the probability of the denatured ensemble to keep knotted is higher for proteins with deeper knots, indicating that knot depth plays a role in determining the topology of the denatured state. Refolding simulations starting from denatured knotted conformations show that not every knot is able to nucleate folding and further indicate that the formation of the knotting loop is a key event in the folding of knotted trefoils. They also show that there are specific native contacts within the knotted core that are crucial to keep a native knotting loop in denatured conformations which otherwise have no detectable structure. The study of the knotting mechanism reveals that the threading of the knotting loop generally occurs towards late folding in conformations that exhibit a significant degree of structural consolidation.
Conflict of interest statement
Figures



 and the unfolding rate slightly above
and the unfolding rate slightly above  . Panel (a) reports the folding rate of the knotted systems and panel (b) reports the folding rate of their unknotted counterparts. Panel (c) reports the unfolding rate of knotted systems, while panel (c) reports the unfolding rate of their unknotted counterparts. The ratio between the folding rate of the deep knot kd and its unfolded counterpart ud is 0.13, and that between the knot k3h and u3h is only 0.05.
. Panel (a) reports the folding rate of the knotted systems and panel (b) reports the folding rate of their unknotted counterparts. Panel (c) reports the unfolding rate of knotted systems, while panel (c) reports the unfolding rate of their unknotted counterparts. The ratio between the folding rate of the deep knot kd and its unfolded counterpart ud is 0.13, and that between the knot k3h and u3h is only 0.05.
 ) and unfolding (
) and unfolding ( ) rates starting from these conformations. The unfolding rate of k12nc is six orders of magnitude smaller than those of the unknotted ones and four orders of magnitude smaller than that of k8nc. In the protein backbones is knotted as in 8knc, the unfolding rate becomes two orders of magnitude smaller with respect to the unknotted conformations.
) rates starting from these conformations. The unfolding rate of k12nc is six orders of magnitude smaller than those of the unknotted ones and four orders of magnitude smaller than that of k8nc. In the protein backbones is knotted as in 8knc, the unfolding rate becomes two orders of magnitude smaller with respect to the unknotted conformations.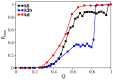
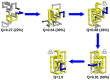
 . The chain terminus closest to the knotted core threads a knotting loop that is already in its native conformation. The hairpin-like terminus only acquires its native conformation after threading.
. The chain terminus closest to the knotted core threads a knotting loop that is already in its native conformation. The hairpin-like terminus only acquires its native conformation after threading.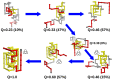
 that corresponds to a malformed conformation with an incorrect crossing of the threading terminus, which nevertheless has a rather native-like knotting loop. Productive threading requires an enlarged and loosen knotting loop and occurs in conformations with fraction of native contacts
that corresponds to a malformed conformation with an incorrect crossing of the threading terminus, which nevertheless has a rather native-like knotting loop. Productive threading requires an enlarged and loosen knotting loop and occurs in conformations with fraction of native contacts  .
.References
-
- King NP, Yeates EO, Yeates TO (2007) Identification of rare slipknots in proteins and their implications for stability and folding. Journal of Molecular Biology 373: 153–166. - PubMed
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources
Other Literature Sources

