Analysis of a scenario for chaotic quantal slowing down of inspiration
- PMID: 24040967
- PMCID: PMC3848870
- DOI: 10.1186/2190-8567-3-18
Analysis of a scenario for chaotic quantal slowing down of inspiration
Abstract
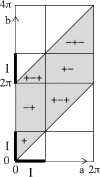
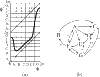
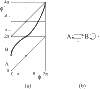
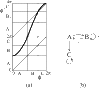
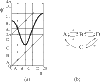
On exposure to opiates, preparations from rat brain stems have been observed to continue to produce regular expiratory signals, but to fail to produce some inspiratory signals. The numbers of expirations between two successive inspirations form an apparently random sequence. Here, we propose an explanation based on the qualitative theory of dynamical systems. A relatively simple scenario for the dynamics of interaction between the generators of expiratory and inspiratory signals produces pseudo-random behaviour of the type observed.
Figures


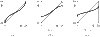
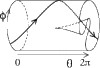



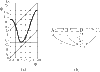


References
LinkOut - more resources
Full Text Sources
Other Literature Sources

