From simple to detailed models for cell polarization

Abstract

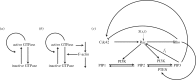
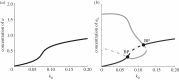
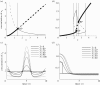
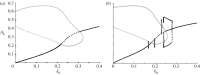
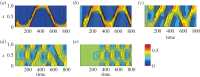
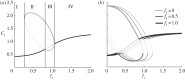
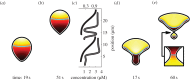
Many mathematical models have been proposed for the process of cell polarization. Some of these are 'functional models' that capture a class of dynamical behaviour, whereas others are derived from features of signalling molecules. Some mechanistic models are detailed, and therefore complex, whereas others are simplified. Each type contributes to our understanding of cell polarization. However, the huge variety at different levels of detail makes comparisons challenging. Here, we provide examples of both elementary and more detailed models for polarization. We also display how a recent mathematical method, local perturbation analysis, can provide an appropriate tool for such comparisons. This technique simplifies and speeds up the model development process by revealing the effect of model extensions, parameter variations and in silico manipulations such as knock-out or over-expression of key molecules. Finally, simulations in both one dimension and two dimensions, and particularly in deforming two-dimensional 'cells', can highlight behaviour not captured by traditional simulation methods.

Keywords: cell polarization; mathematical analysis; pattern formation; reaction–diffusion equations.

Figure 1.

Schematics for a succession of simple to complex models based on reacting and diffusing components. (a) Wave-pinning (WP) model [2]. (b) The WP model is linked to F-actin via feedback, based on Holmes et al. [3]. (c) Full model of Cdc42, Rac and Rho from Holmes et al. [, fig. 1d] (with permission of PLOS Computational Biology).

Figure 2.

(a) Bifurcation diagram of the well-mixed WP system (equation (3.2)) with the kinetics (equation (4.1)). The steady-state value of u is plotted with respect to a basal activation rate, k₀. Parameter values n = 2, γ = 1, u₀ = 1, δ = 1 and total average concentration w = 2.2683. (b) LPA diagram of the WP system (same parameter values). This diagram forms a ‘signature’ for the model. It also provides information about distinct behaviours possible in various parameter regimes. BP indicates a branch point bifurcation. See text for details.

Figure 3.

A comparison of LPA diagrams for (a) Otsuji [19] and (b) WP [2] models, showing u_L with the total average concentration and w as the bifurcation parameter. (a) Otsuji kinetics (equation (4.2)) with a₁ = 25, a₂ = 0.7. There is a single bifurcation at w = 1.429. (b) WP kinetics (equation (4.1)) with k₀ = 0.067, γ = 1, u₀ = 1, δ = 1, n = 2. Bifurcations are at branch points (transcritical): w = 2.3, 2.6; limit points (fold): w = 1.91, 3.55. The behaviour of the model can be classified into regimes (separated by thin vertical lines): Region I: 0 < w < 1.91, II: 1.91 < w < 2.3, III: 2.3 < w < 2.6, IIb: 2.6 < w < 3.55 and IV: 3.55 < w. BP indicates a branch point bifurcation. (c,d) A series of spatial profiles at increasing times T of the full RD PDEs for (c) the Otsuji kinetics (equation (4.2)) with w = 2 in the Turing regime (patterning initiated by numerical noise) and (d) the WP kinetics (equation (4.1)) with w = 2.2 demonstrating wave-pinning behaviour (a pulse at t = 20 initiates patterning).

Figure 4.

LPA bifurcation diagram reveals the effect of model extension from WP to WP-F (figure 1a,b). (a) WP system alone, showing active GTPase A_L versus basal activation rate k₀. Here, F-actin is treated as a parameter (F = 5) in the system (equations (4.3)) with kinetics f(A,I,F) given by equation (4.4). Transcritical bifurcations occur at k₀ = 0.2178, 0.3051 (branch points) and fold bifurcation at k₀ = 0.3229 (limit point). (b) As in (a) but with F-actin as a dynamic variable. Note new Hopf bifurcations at k₀ = 0.169, 0.1963, 0.2318, 0.2419, 0.2799. (The outer two of these are on the global branch.) These indicate presence of oscillatory behaviour. Transcritical bifurcations are seen at k₀ = 0.1814, 0.25, and there is a fold bifurcation at k₀ = 0.2586. Parameters values: A₀ = 0.4, γ = 1.0, s₁ = 0.7, s₂ = 0.7, T = 1, ε = 0.1, k_n = 2.0, k_s = 0.25.

Figure 5.

Full simulations of the WP-F model (equations (4.3) and (4.4)) showing A(x,t). A variety of waves and periodic travelling patterns are obtained. Parameter values as in figure 4b, with (a) k₀ = 0.1, (b) k₀ = 0.175, (c) k₀ = 0.22, (d) k₀ = 0.24, and (e) k₀ = 0.25.

Figure 6.

(a) LPA bifurcation diagram of the models shown in Holmes et al. [, fig. 1c]. The value of Cdc42 C_l is plotted versus a basal Rac activation rate I_r. (b) Same diagram showing the effect of feedback from the PIPs to Rac. Adapted from [, figs 3 and 6a] with permission of PLOS Computational Biology.

Figure 7.

For default parameters (figure 3b), simple coupling of WP to cell boundary velocity (equation (6.1)) yields transient deformation (b,c), followed by steady translation (from (e) onwards), starting from a fully polarized circular cell (a). Boundary motion for OT with default parameters (figure 3a) yields rapid constriction (g–i) without significant translation. Concentration profiles along the vertical symmetry axis of each cell are shown for the WP case (e), whereas only the initial (solid) and final (dashed) profiles are shown for the OT case (j). For each cell, the polymerization threshold u* is shown as a cyan contour.

Figure 8.

Unconstricted, convex cells (a,b), result when the default reaction rate for OT is replaced with a lower value (a₁ = 1 s⁻¹). Constricted, concave cells (e,f) result when default WP reaction rates are replaced with higher values (δ = γ = 5 s⁻¹). Concentration profiles along the vertical symmetry axis of each cell (c) use different scales, with concentrations for WP (black curves) along the top edge of the graph and concentrations for OT (grey curves) along the bottom. For each cell, the polymerization threshold u* is shown as a cyan contour.