From birdsong to human speech recognition: bayesian inference on a hierarchy of nonlinear dynamical systems
- PMID: 24068902
- PMCID: PMC3772045
- DOI: 10.1371/journal.pcbi.1003219
From birdsong to human speech recognition: bayesian inference on a hierarchy of nonlinear dynamical systems
Abstract
Our knowledge about the computational mechanisms underlying human learning and recognition of sound sequences, especially speech, is still very limited. One difficulty in deciphering the exact means by which humans recognize speech is that there are scarce experimental findings at a neuronal, microscopic level. Here, we show that our neuronal-computational understanding of speech learning and recognition may be vastly improved by looking at an animal model, i.e., the songbird, which faces the same challenge as humans: to learn and decode complex auditory input, in an online fashion. Motivated by striking similarities between the human and songbird neural recognition systems at the macroscopic level, we assumed that the human brain uses the same computational principles at a microscopic level and translated a birdsong model into a novel human sound learning and recognition model with an emphasis on speech. We show that the resulting Bayesian model with a hierarchy of nonlinear dynamical systems can learn speech samples such as words rapidly and recognize them robustly, even in adverse conditions. In addition, we show that recognition can be performed even when words are spoken by different speakers and with different accents-an everyday situation in which current state-of-the-art speech recognition models often fail. The model can also be used to qualitatively explain behavioral data on human speech learning and derive predictions for future experiments.
Conflict of interest statement
The authors have declared that no competing interests exist.
Figures


 and
and  , respectively) try to minimize the precision-weighted prediction errors (
, respectively) try to minimize the precision-weighted prediction errors ( and
and  ) by exchanging messages. Predictions are transferred from second level to the first and prediction error is propagated back from the first to the second level (see section Model: Learning and Recognition for more details). Adapted from .
) by exchanging messages. Predictions are transferred from second level to the first and prediction error is propagated back from the first to the second level (see section Model: Learning and Recognition for more details). Adapted from .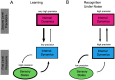




 and internal log-precision:
and internal log-precision:  where
where  from left to right). For each precision ratio, we plotted the reduction in prediction error (of the causal states, see Model) after five repetitions of the word “eight” spoken with a New Zealand accent. As expected, accent adaptation was accomplished only with high sensory/internal precision ratios (resulting in greatly reduced prediction errors) whereas no adaptation occurred (prediction errors remained high) when this ratio was low.
from left to right). For each precision ratio, we plotted the reduction in prediction error (of the causal states, see Model) after five repetitions of the word “eight” spoken with a New Zealand accent. As expected, accent adaptation was accomplished only with high sensory/internal precision ratios (resulting in greatly reduced prediction errors) whereas no adaptation occurred (prediction errors remained high) when this ratio was low.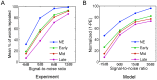
Similar articles
-
A hierarchical neuronal model for generation and online recognition of birdsongs.PLoS Comput Biol. 2011 Dec;7(12):e1002303. doi: 10.1371/journal.pcbi.1002303. Epub 2011 Dec 15. PLoS Comput Biol. 2011. PMID: 22194676 Free PMC article.
-
Sound sequences in birdsong: how much do birds really care?Philos Trans R Soc Lond B Biol Sci. 2020 Jan 6;375(1789):20190044. doi: 10.1098/rstb.2019.0044. Epub 2019 Nov 18. Philos Trans R Soc Lond B Biol Sci. 2020. PMID: 31735149 Free PMC article. Review.
-
Recognizing recurrent neural networks (rRNN): Bayesian inference for recurrent neural networks.Biol Cybern. 2012 Jul;106(4-5):201-17. doi: 10.1007/s00422-012-0490-x. Epub 2012 May 12. Biol Cybern. 2012. PMID: 22581026
-
Songbirds can learn flexible contextual control over syllable sequencing.Elife. 2021 Jun 1;10:e61610. doi: 10.7554/eLife.61610. Elife. 2021. PMID: 34060473 Free PMC article.
-
Brains for birds and babies: Neural parallels between birdsong and speech acquisition.Neurosci Biobehav Rev. 2017 Oct;81(Pt B):225-237. doi: 10.1016/j.neubiorev.2016.12.035. Epub 2017 Jan 10. Neurosci Biobehav Rev. 2017. PMID: 28087242 Review.
Cited by
-
A general auditory bias for handling speaker variability in speech? Evidence in humans and songbirds.Front Psychol. 2015 Aug 25;6:1243. doi: 10.3389/fpsyg.2015.01243. eCollection 2015. Front Psychol. 2015. PMID: 26379579 Free PMC article.
-
Active Inference and Cooperative Communication: An Ecological Alternative to the Alignment View.Front Psychol. 2021 Aug 12;12:708780. doi: 10.3389/fpsyg.2021.708780. eCollection 2021. Front Psychol. 2021. PMID: 34456822 Free PMC article.
-
Learning of Chunking Sequences in Cognition and Behavior.PLoS Comput Biol. 2015 Nov 19;11(11):e1004592. doi: 10.1371/journal.pcbi.1004592. eCollection 2015 Nov. PLoS Comput Biol. 2015. PMID: 26584306 Free PMC article.
-
Applied physics: A new spin on nanoscale computing.Nature. 2017 Jul 26;547(7664):407-408. doi: 10.1038/547407a. Nature. 2017. PMID: 28748927 No abstract available.
-
A model of individualized canonical microcircuits supporting cognitive operations.PLoS One. 2017 Dec 4;12(12):e0188003. doi: 10.1371/journal.pone.0188003. eCollection 2017. PLoS One. 2017. PMID: 29200435 Free PMC article.
References
-
- Bolhuis JJ, Okanoya K, Scharff C (2010) Twitter evolution: converging mechanisms in birdsong and human speech. Nature Reviews Neuroscience 11: 747–759. - PubMed
-
- Doupe AJ, Kuhl PK (1999) Birdsong and human speech: Common themes and mechanisms. Annual Review of Neuroscience 22: 567–631. - PubMed
-
- Creutzfeldt O, Ojemann G, Lettich E (1989) Neuronal-Activity in the Human Lateral Temporal-Lobe .1. Responses to Speech. Experimental Brain Research 77: 451–475. - PubMed
-
- Berwick RC, Okanoya K, Beckers GJL, Bolhuis JJ (2011) Songs to syntax: the linguistics of birdsong. Trends in Cognitive Sciences 15: 113–121. - PubMed
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources

