Target inhibition networks: predicting selective combinations of druggable targets to block cancer survival pathways
- PMID: 24068907
- PMCID: PMC3772058
- DOI: 10.1371/journal.pcbi.1003226
Target inhibition networks: predicting selective combinations of druggable targets to block cancer survival pathways
Abstract
A recent trend in drug development is to identify drug combinations or multi-target agents that effectively modify multiple nodes of disease-associated networks. Such polypharmacological effects may reduce the risk of emerging drug resistance by means of attacking the disease networks through synergistic and synthetic lethal interactions. However, due to the exponentially increasing number of potential drug and target combinations, systematic approaches are needed for prioritizing the most potent multi-target alternatives on a global network level. We took a functional systems pharmacology approach toward the identification of selective target combinations for specific cancer cells by combining large-scale screening data on drug treatment efficacies and drug-target binding affinities. Our model-based prediction approach, named TIMMA, takes advantage of the polypharmacological effects of drugs and infers combinatorial drug efficacies through system-level target inhibition networks. Case studies in MCF-7 and MDA-MB-231 breast cancer and BxPC-3 pancreatic cancer cells demonstrated how the target inhibition modeling allows systematic exploration of functional interactions between drugs and their targets to maximally inhibit multiple survival pathways in a given cancer type. The TIMMA prediction results were experimentally validated by means of systematic siRNA-mediated silencing of the selected targets and their pairwise combinations, showing increased ability to identify not only such druggable kinase targets that are essential for cancer survival either individually or in combination, but also synergistic interactions indicative of non-additive drug efficacies. These system-level analyses were enabled by a novel model construction method utilizing maximization and minimization rules, as well as a model selection algorithm based on sequential forward floating search. Compared with an existing computational solution, TIMMA showed both enhanced prediction accuracies in cross validation as well as significant reduction in computation times. Such cost-effective computational-experimental design strategies have the potential to greatly speed-up the drug testing efforts by prioritizing those interventions and interactions warranting further study in individual cancer cases.
Conflict of interest statement
The authors have declared that no competing interests exist.
Figures
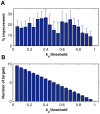
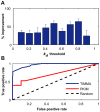
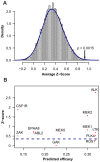
 thresholds to binarize the simulated binding affinity data.
thresholds to binarize the simulated binding affinity data.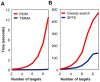
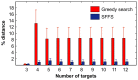
 targets,
targets,  . (B) Running time of the greedy search and the sequential forward floating search (SFFS) algorithms when reaching an optimal cancer-specific target set of size
. (B) Running time of the greedy search and the sequential forward floating search (SFFS) algorithms when reaching an optimal cancer-specific target set of size  .
.
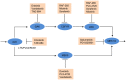
 is shown inside the node, while the other equivalent kinase targets are shown beside the meta-target node. Red squares list available drugs that inhibit the corresponding target nodes. Data and detailed results are provided in Dataset S7.
is shown inside the node, while the other equivalent kinase targets are shown beside the meta-target node. Red squares list available drugs that inhibit the corresponding target nodes. Data and detailed results are provided in Dataset S7.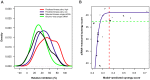
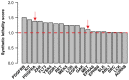
 where a = 41, b = 0.23, c = 0.02.
where a = 41, b = 0.23, c = 0.02.Similar articles
-
Validation of a network-based strategy for the optimization of combinatorial target selection in breast cancer therapy: siRNA knockdown of network targets in MDA-MB-231 cells as an in vitro model for inhibition of tumor development.Oncotarget. 2016 Sep 27;7(39):63189-63203. doi: 10.18632/oncotarget.11055. Oncotarget. 2016. PMID: 27527857 Free PMC article.
-
Network pharmacology strategies toward multi-target anticancer therapies: from computational models to experimental design principles.Curr Pharm Des. 2014;20(1):23-36. doi: 10.2174/13816128113199990470. Curr Pharm Des. 2014. PMID: 23530504 Free PMC article. Review.
-
TIMMA-R: an R package for predicting synergistic multi-targeted drug combinations in cancer cell lines or patient-derived samples.Bioinformatics. 2015 Jun 1;31(11):1866-8. doi: 10.1093/bioinformatics/btv067. Epub 2015 Jan 31. Bioinformatics. 2015. PMID: 25638808 Free PMC article.
-
Network pharmacology modeling identifies synergistic Aurora B and ZAK interaction in triple-negative breast cancer.NPJ Syst Biol Appl. 2019 Jul 8;5:20. doi: 10.1038/s41540-019-0098-z. eCollection 2019. NPJ Syst Biol Appl. 2019. PMID: 31312514 Free PMC article.
-
Improvement of conventional anti-cancer drugs as new tools against multidrug resistant tumors.Drug Resist Updat. 2020 May;50:100682. doi: 10.1016/j.drup.2020.100682. Epub 2020 Feb 7. Drug Resist Updat. 2020. PMID: 32087558
Cited by
-
A 35-gene signature discriminates between rapidly- and slowly-progressing glioblastoma multiforme and predicts survival in known subtypes of the cancer.BMC Cancer. 2018 Apr 3;18(1):377. doi: 10.1186/s12885-018-4103-5. BMC Cancer. 2018. PMID: 29614978 Free PMC article.
-
1,3,4-Oxadiazole: An Emerging Scaffold to Inhibit the Thymidine Phosphorylase as an Anticancer Agent.Curr Med Chem. 2024;31(38):6227-6250. doi: 10.2174/0929867331666230712113943. Curr Med Chem. 2024. PMID: 37438902 Review.
-
DrugCombDB: a comprehensive database of drug combinations toward the discovery of combinatorial therapy.Nucleic Acids Res. 2020 Jan 8;48(D1):D871-D881. doi: 10.1093/nar/gkz1007. Nucleic Acids Res. 2020. PMID: 31665429 Free PMC article.
-
Quantitative scoring of differential drug sensitivity for individually optimized anticancer therapies.Sci Rep. 2014 Jun 5;4:5193. doi: 10.1038/srep05193. Sci Rep. 2014. PMID: 24898935 Free PMC article.
-
Screening lifespan-extending drugs in Caenorhabditis elegans via label propagation on drug-protein networks.BMC Syst Biol. 2016 Dec 23;10(Suppl 4):131. doi: 10.1186/s12918-016-0362-4. BMC Syst Biol. 2016. PMID: 28155715 Free PMC article.
References
-
- Pammolli F, Magazzini L, Riccaboni M (2011) The productivity crisis in pharmaceutical R&D. Nature Reviews Drug Discovery 10: 428–438 doi:10.1038/nrd3405 - DOI - PubMed
-
- Hutchinson L, Kirk R (2011) High drug attrition rates—where are we going wrong? Nature Reviews Clinical Oncology 8: 189–190 doi:10.1038/nrclinonc.2011.34 - DOI - PubMed
-
- Hopkins AL (2008) Network pharmacology: the next paradigm in drug discovery. Nat Chem Biol 4: 682–690 doi:10.1038/nchembio.118 - DOI - PubMed
-
- Jia J, Zhu F, Ma X, Cao Z, Cao ZW, et al. (2009) Mechanisms of drug combinations: interaction and network perspectives. Nat Rev Drug Discov 8: 111–128 doi:10.1038/nrd2683 - DOI - PubMed
-
- Al-Lazikani B, Banerji U, Workman P (2012) Combinatorial drug therapy for cancer in the post-genomic era. Nat Biotechnol 30: 679–692 doi:10.1038/nbt.2284 - DOI - PubMed
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources
Other Literature Sources
Miscellaneous

