Survival analysis of irish amyotrophic lateral sclerosis patients diagnosed from 1995-2010
- PMID: 24098664
- PMCID: PMC3786977
- DOI: 10.1371/journal.pone.0074733
Survival analysis of irish amyotrophic lateral sclerosis patients diagnosed from 1995-2010
Abstract
Introduction: The Irish ALS register is a valuable resource for examining survival factors in Irish ALS patients. Cox regression has become the default tool for survival analysis, but recently new classes of flexible parametric survival analysis tools known as Royston-Parmar models have become available.
Methods: We employed Cox proportional hazards and Royston-Parmar flexible parametric modeling to examine factors affecting survival in Irish ALS patients. We further examined the effect of choice of timescale on Cox models and the proportional hazards assumption, and extended both Cox and Royston-Parmar models with time varying components.
Results: On comparison of models we chose a Royston-Parmar proportional hazards model without time varying covariates as the best fit. Using this model we confirmed the association of known survival markers in ALS including age at diagnosis (Hazard Ratio (HR) 1.34 per 10 year increase; 95% CI 1.26-1.42), diagnostic delay (HR 0.96 per 12 weeks delay; 95% CI 0.94-0.97), Definite ALS (HR 1.47 95% CI 1.17-1.84), bulbar onset disease (HR 1.58 95% CI 1.33-1.87), riluzole use (HR 0.72 95% CI 0.61-0.85) and attendance at an ALS clinic (HR 0.74 95% CI 0.64-0.86).
Discussion: Our analysis explored the strengths and weaknesses of Cox proportional hazard and Royston-Parmar flexible parametric methods. By including time varying components we were able to gain deeper understanding of the dataset. Variation in survival between time periods appears to be due to missing data in the first time period. The use of age as timescale to account for confounding by age resolved breaches of the proportional hazards assumption, but in doing so may have obscured deficiencies in the data. Our study demonstrates the need to test for, and fully explore, breaches of the Cox proportional hazards assumption. Royston-Parmar flexible parametric modeling proved a powerful method for achieving this.
Conflict of interest statement
Figures

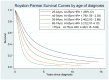

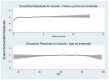
References
-
- Hardiman O, van den Berg LH, Kiernan MC (2011) Clinical diagnosis and management of amyotrophic lateral sclerosis. Nature reviews Neurology 7: 639–649. PMID: 21989247. - PubMed
-
- Traynor BJ, Codd MB, Corr B, Forde C, Frost E, et al... (1999) Incidence and prevalence of ALS in Ireland, 1995–1997: A population-based study. Neurology 52: 504–504. PMID: 10025778. - PubMed
-
- Elamin M, Phukan J, Bede P, Jordan N, Byrne S, et al... (2011) Executive dysfunction is a negative prognostic indicator in patients with ALS without dementia. Neurology 76: 1263–1269. PMID: 21464431. - PubMed
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources
Medical
Miscellaneous

