Host-parasitoid dynamics and the success of biological control when parasitoids are prone to allee effects
- PMID: 24116153
- PMCID: PMC3792096
- DOI: 10.1371/journal.pone.0076768
Host-parasitoid dynamics and the success of biological control when parasitoids are prone to allee effects
Abstract
In sexual organisms, low population density can result in mating failures and subsequently yields a low population growth rate and high chance of extinction. For species that are in tight interaction, as in host-parasitoid systems, population dynamics are primarily constrained by demographic interdependences, so that mating failures may have much more intricate consequences. Our main objective is to study the demographic consequences of parasitoid mating failures at low density and its consequences on the success of biological control. For this, we developed a deterministic host-parasitoid model with a mate-finding Allee effect, allowing to tackle interactions between the Allee effect and key determinants of host-parasitoid demography such as the distribution of parasitoid attacks and host competition. Our study shows that parasitoid mating failures at low density result in an extinction threshold and increase the domain of parasitoid deterministic extinction. When proned to mate finding difficulties, parasitoids with cyclic dynamics or low searching efficiency go extinct; parasitoids with high searching efficiency may either persist or go extinct, depending on host intraspecific competition. We show that parasitoids suitable as biocontrol agents for their ability to reduce host populations are particularly likely to suffer from mate-finding Allee effects. This study highlights novel perspectives for understanding of the dynamics observed in natural host-parasitoid systems and improving the success of parasitoid introductions.
Conflict of interest statement
Figures


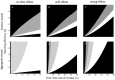

 ,
,  ,
,  ,
,  ; b)
; b)  ,
,  ,
,  ,
,  ; c)
; c)  ,
,  ,
,  ,
,  . The black curve on parasitoid graphics represents
. The black curve on parasitoid graphics represents  .
.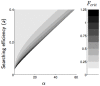
 ,
,  , K = 500.
, K = 500.
 )
)Similar articles
-
A discrete-time host-parasitoid model with an Allee effect.J Biol Dyn. 2015;9:34-51. doi: 10.1080/17513758.2014.982219. J Biol Dyn. 2015. PMID: 25431970
-
Invading parasitoids suffer no Allee effect: a manipulative field experiment.Ecology. 2007 Sep;88(9):2392-403. doi: 10.1890/06-1238.1. Ecology. 2007. PMID: 17918416
-
A host-parasitoid system with predation-driven component Allee effects in host population.J Biol Dyn. 2015;9 Suppl 1:213-32. doi: 10.1080/17513758.2014.972473. Epub 2014 Oct 23. J Biol Dyn. 2015. PMID: 25340591
-
Functional ecology of immature parasitoids.Annu Rev Entomol. 2004;49:27-49. doi: 10.1146/annurev.ento.49.061703.153618. Annu Rev Entomol. 2004. PMID: 14651455 Review.
-
Single-species models of the Allee effect: extinction boundaries, sex ratios and mate encounters.J Theor Biol. 2002 Oct 7;218(3):375-94. doi: 10.1006/jtbi.2002.3084. J Theor Biol. 2002. PMID: 12381437 Review.
Cited by
-
Augmentative biocontrol when natural enemies are subject to Allee effects.J Math Biol. 2017 Jun;74(7):1561-1587. doi: 10.1007/s00285-016-1063-8. Epub 2016 Oct 6. J Math Biol. 2017. PMID: 27714431
-
Sterile males in a parasitoid wasp with complementary sex determination: from fitness costs to population extinction.BMC Ecol. 2015 May 12;15:13. doi: 10.1186/s12898-014-0032-6. BMC Ecol. 2015. PMID: 25962498 Free PMC article.
-
Parasitism and Food Web Structure in Defoliating Lepidoptera - Parasitoid Communities on Soybean.Neotrop Entomol. 2016 Dec;45(6):712-717. doi: 10.1007/s13744-016-0416-8. Epub 2016 Jun 14. Neotrop Entomol. 2016. PMID: 27299866
-
Best Timing to Determine Field Parasitism by Released Diachasmimorpha longicaudata (Hymenoptera: Braconidae) Against Anastrepha (Diptera: Tephritidae) Pest Populations.Neotrop Entomol. 2019 Feb;48(1):143-151. doi: 10.1007/s13744-018-0622-7. Epub 2018 Jul 25. Neotrop Entomol. 2019. PMID: 30047024
-
Integrated Pest Management in a Predator-Prey System with Allee Effects.Neotrop Entomol. 2015 Aug;44(4):385-91. doi: 10.1007/s13744-015-0297-2. Epub 2015 Jun 5. Neotrop Entomol. 2015. PMID: 26045054
References
-
- Nicholson AJ, Bailey VA (1935) The balance of animal populations. P Zool Soc Lond 3: 551–593.
-
- Hassell MP (2000) Host-parasitoid population dynamics. J Anim Ecol 69: 543–566. - PubMed
-
- Bernstein C (2000) Host-parasitoid models: the story of a successful failure. in Hochberg ME and Ives AR Parasitoid population biology.Princeton University Press, Princeton. pp. 41–57.
-
- Bellows T (2001) Restoring population balance through natural enemy introduction. Biol Control 21: 199–205.
-
- Hall RW, Ehler LE (1979) Rate of establishment of natural enemies in classical biological control. Bull Entomol Soc Am 25: 280–283.
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources

