Sampling scheme and compressed sensing applied to solid-state NMR spectroscopy
- PMID: 24140622
- PMCID: PMC3851314
- DOI: 10.1016/j.jmr.2013.09.013
Sampling scheme and compressed sensing applied to solid-state NMR spectroscopy
Abstract
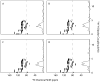
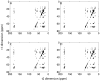
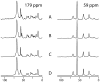
We describe the incorporation of non-uniform sampling (NUS) compressed sensing (CS) into oriented sample (OS) solid-state NMR for stationary aligned samples and magic angle spinning (MAS) Solid-state NMR for unoriented 'powder' samples. Both simulated and experimental results indicate that 25-33% of a full linearly sampled data set is required to reconstruct two- and three-dimensional solid-state NMR spectra with high fidelity. A modest increase in signal-to-noise ratio accompanies the reconstruction.
Keywords: Compressed sensing; Membrane proteins; Non-uniform sampling; Oriented samples; Protein NMR; Sensitivity; Solid-state NMR.
Copyright © 2013 Elsevier Inc. All rights reserved.
Figures



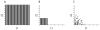



Similar articles
-
Accurate scoring of non-uniform sampling schemes for quantitative NMR.J Magn Reson. 2014 Sep;246:31-5. doi: 10.1016/j.jmr.2014.06.020. Epub 2014 Jul 2. J Magn Reson. 2014. PMID: 25063954 Free PMC article.
-
Reducing seed dependent variability of non-uniformly sampled multidimensional NMR data.J Magn Reson. 2015 Jul;256:60-69. doi: 10.1016/j.jmr.2015.04.003. Epub 2015 Apr 25. J Magn Reson. 2015. PMID: 26004701
-
Sensitivity enhancement of NMR spectra of half-integer spin quadrupolar nuclei in solids using hyperbolic secant pulses.J Magn Reson. 2007 Jan;184(1):85-100. doi: 10.1016/j.jmr.2006.09.007. Epub 2006 Oct 13. J Magn Reson. 2007. PMID: 17046297
-
Solid-state NMR structures of integral membrane proteins.Mol Membr Biol. 2015 Aug-Dec;32(5-8):156-78. doi: 10.3109/09687688.2016.1139754. Epub 2016 Feb 8. Mol Membr Biol. 2015. PMID: 26857803 Review.
-
Recent advances in magic angle spinning solid state NMR of membrane proteins.Prog Nucl Magn Reson Spectrosc. 2014 Oct;82:1-26. doi: 10.1016/j.pnmrs.2014.07.001. Epub 2014 Jul 26. Prog Nucl Magn Reson Spectrosc. 2014. PMID: 25444696 Review.
Cited by
-
Small Molecule Accurate Recognition Technology (SMART) to Enhance Natural Products Research.Sci Rep. 2017 Oct 27;7(1):14243. doi: 10.1038/s41598-017-13923-x. Sci Rep. 2017. PMID: 29079836 Free PMC article.
-
Structural and functional consequences of the H180A mutation of the light-driven sodium pump KR2.Biophys J. 2023 Mar 21;122(6):1003-1017. doi: 10.1016/j.bpj.2022.12.023. Epub 2022 Dec 17. Biophys J. 2023. PMID: 36528791 Free PMC article.
-
Non-Uniform Sampling in NMR Spectroscopy and the Preservation of Spectral Knowledge in the Time and Frequency Domains.J Phys Chem A. 2020 Jul 2;124(26):5474-5486. doi: 10.1021/acs.jpca.0c02930. Epub 2020 Jun 18. J Phys Chem A. 2020. PMID: 32496067 Free PMC article.
-
Efficient route to high-bandwidth nanoscale magnetometry using single spins in diamond.Sci Rep. 2014 Apr 14;4:4677. doi: 10.1038/srep04677. Sci Rep. 2014. PMID: 24728454 Free PMC article.
-
Gd3+-chelated lipid accelerates solid-state NMR spectroscopy of seven-transmembrane proteins.J Biomol NMR. 2017 Jul;68(3):203-214. doi: 10.1007/s10858-017-0120-y. Epub 2017 May 30. J Biomol NMR. 2017. PMID: 28560567
References
-
- Hu KN, Bajaj VS, Rosay M, Griffin RG. High-frequency dynamic nuclear polarization using mixtures of TEMPO and trityl radicals. J Chem Phys. 2007;126:044512–7. - PubMed
-
- Hall DA, Maus DC, Gerfen GJ, Inati SJ, Becerra LR, Dahlquist FW, Griffin RG. Polarization-Enhanced NMR Spectroscopy of Biomolecules in Frozen Solution. Science. 1997;276:930–932. - PubMed
-
- Joo CG, Hu KN, Bryant JA, Griffin RG. In Situ Temperature Jump High-Frequency Dynamic Nuclear Polarization Experiments: Enhanced Sensitivity in Liquid-State NMR Spectroscopy. J Am Chem Soc. 2006;128:9428–9432. - PubMed
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

