Form-finding model shows how cytoskeleton network stiffness is realized
- PMID: 24146992
- PMCID: PMC3798660
- DOI: 10.1371/journal.pone.0077417
Form-finding model shows how cytoskeleton network stiffness is realized
Abstract
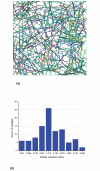
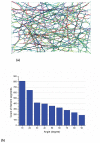
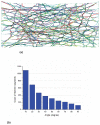
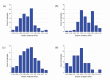
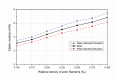
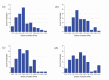
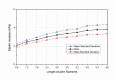
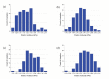
In eukaryotic cells the actin-cytoskeletal network provides stiffness and the driving force that contributes to changes in cell shape and cell motility, but the elastic behavior of this network is not well understood. In this paper a two dimensional form-finding model is proposed to investigate the elasticity of the actin filament network. Utilizing an initially random array of actin filaments and actin-cross-linking proteins the form-finding model iterates until the random array is brought into a stable equilibrium configuration. With some care given to actin filament density and length, distance between host sites for cross-linkers, and overall domain size the resulting configurations from the form-finding model are found to be topologically similar to cytoskeletal networks in real cells. The resulting network may then be mechanically exercised to explore how the actin filaments deform and align under load and the sensitivity of the network's stiffness to actin filament density, length, etc. Results of the model are consistent with the experimental literature, e.g. actin filaments tend to re-orient in the direction of stretching; and the filament relative density, filament length, and actin-cross-linking protein's relative density, control the actin-network stiffness. The model provides a ready means of extension to more complicated domains and a three-dimensional form-finding model is under development as well as models studying the formation of actin bundles.
Conflict of interest statement
Figures

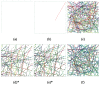
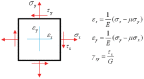
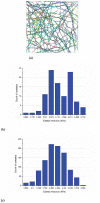
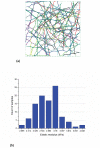





Similar articles
-
Discontinuous unbinding transitions of filament bundles.Phys Rev Lett. 2005 Jul 15;95(3):038102. doi: 10.1103/PhysRevLett.95.038102. Epub 2005 Jul 14. Phys Rev Lett. 2005. PMID: 16090774
-
Cytoskeletal bundle mechanics.Biophys J. 2008 Apr 15;94(8):2955-64. doi: 10.1529/biophysj.107.119743. Epub 2007 Nov 30. Biophys J. 2008. PMID: 18055529 Free PMC article.
-
A mechanochemical model of actin filaments.Biophys J. 2012 Aug 22;103(4):719-27. doi: 10.1016/j.bpj.2012.07.020. Biophys J. 2012. PMID: 22947933 Free PMC article.
-
Cytoskeletal tropomyosins: choreographers of actin filament functional diversity.J Muscle Res Cell Motil. 2013 Aug;34(3-4):261-74. doi: 10.1007/s10974-013-9355-8. Epub 2013 Aug 1. J Muscle Res Cell Motil. 2013. PMID: 23904035 Free PMC article. Review.
-
Cytoskeletal crosstalk: when three different personalities team up.Curr Opin Cell Biol. 2015 Feb;32:39-47. doi: 10.1016/j.ceb.2014.10.005. Epub 2014 Nov 15. Curr Opin Cell Biol. 2015. PMID: 25460780 Review.
Cited by
-
Multiscale analysis of architecture, cell size and the cell cortex reveals cortical F-actin density and composition are major contributors to mechanical properties during convergent extension.Development. 2018 Oct 5;145(19):dev161281. doi: 10.1242/dev.161281. Development. 2018. PMID: 30190279 Free PMC article.
References
-
- Ethier CR, Simmons CA (2007) Introductory biomechanics: from cells to organisms. Cambridge Univ Pr.
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources

