Resolving social conflict among females without overt aggression
- PMID: 24167306
- PMCID: PMC3826205
- DOI: 10.1098/rstb.2013.0076
Resolving social conflict among females without overt aggression
Abstract
Members of animal societies compete over resources and reproduction, but the extent to which such conflicts of interest are resolved peacefully (without recourse to costly or wasteful acts of aggression) varies widely. Here, we describe two theoretical mechanisms that can help to understand variation in the incidence of overt behavioural conflict: (i) destruction competition and (ii) the use of threats. The two mechanisms make different assumptions about the degree to which competitors are socially sensitive (responsive to real-time changes in the behaviour of their social partners). In each case, we discuss how the model assumptions relate to biological reality and highlight the genetic, ecological and informational factors that are likely to promote peaceful conflict resolution, drawing on empirical examples. We suggest that, relative to males, reproductive conflict among females may be more frequently resolved peacefully through threats of punishment, rather than overt acts of punishment, because (i) offspring are more costly to produce for females and (ii) reproduction is more difficult to conceal. The main need now is for empirical work to test whether the mechanisms described here can indeed explain how social conflict can be resolved without overt aggression.
Keywords: conflict resolution; evolution of cooperation; fighting; negotiation; reproductive skew; threats.
Figures
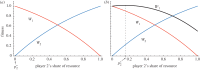
 ). In the case shown q = 1. If the two players are non-relatives (as in (a)), the optimal division of resources from the perspective of player 1 is
). In the case shown q = 1. If the two players are non-relatives (as in (a)), the optimal division of resources from the perspective of player 1 is  , and from the perspective of player 2 is
, and from the perspective of player 2 is  . Thus, the zone of conflict or ‘battleground’ in the case of competition between non-relatives is simply all of the available resource. (b) The case where the two players are genetic relatives (specifically, in the plot we assume r = 0.5). IF1 is the inclusive fitness payoff of player 1 (calculated as W1 + r W2). The optimum division of the resource for player 1 is the value of p2 which maximizes IF1, i.e. the value which solves the equation ∂IF1/∂p2 = 0. Given our chosen fitness functions, the solution for player 1's optimal allocation is
. Thus, the zone of conflict or ‘battleground’ in the case of competition between non-relatives is simply all of the available resource. (b) The case where the two players are genetic relatives (specifically, in the plot we assume r = 0.5). IF1 is the inclusive fitness payoff of player 1 (calculated as W1 + r W2). The optimum division of the resource for player 1 is the value of p2 which maximizes IF1, i.e. the value which solves the equation ∂IF1/∂p2 = 0. Given our chosen fitness functions, the solution for player 1's optimal allocation is  ; and (since the players are symmetrical) for player 2 the optimal allocation is one minus this expression, i.e. 1/2 − (ln r)/2q. Thus, the battleground of conflict is 1/2 ± (ln r)/2q. Note that the value of the resource V has no effect on the width of the battleground. The lower and upper bounds of the battleground get closer together as r increases and as q increases. In other words, increasing relatedness and increasing ‘bowedness’ of the fitness function draw together the fitness optima of competitors, reducing the scope for evolutionary conflict.
; and (since the players are symmetrical) for player 2 the optimal allocation is one minus this expression, i.e. 1/2 − (ln r)/2q. Thus, the battleground of conflict is 1/2 ± (ln r)/2q. Note that the value of the resource V has no effect on the width of the battleground. The lower and upper bounds of the battleground get closer together as r increases and as q increases. In other words, increasing relatedness and increasing ‘bowedness’ of the fitness function draw together the fitness optima of competitors, reducing the scope for evolutionary conflict.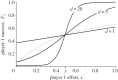

Similar articles
-
Female competition and its evolutionary consequences in mammals.Biol Rev Camb Philos Soc. 2011 May;86(2):341-66. doi: 10.1111/j.1469-185X.2010.00149.x. Biol Rev Camb Philos Soc. 2011. PMID: 20636474 Review.
-
Proximate perspectives on the evolution of female aggression: good for the gander, good for the goose?Philos Trans R Soc Lond B Biol Sci. 2013 Oct 28;368(1631):20130083. doi: 10.1098/rstb.2013.0083. Print 2013. Philos Trans R Soc Lond B Biol Sci. 2013. PMID: 24167313 Free PMC article. Review.
-
Family feuds: social competition and sexual conflict in complex societies.Philos Trans R Soc Lond B Biol Sci. 2012 Aug 19;367(1600):2304-13. doi: 10.1098/rstb.2011.0283. Philos Trans R Soc Lond B Biol Sci. 2012. PMID: 22777018 Free PMC article. Review.
-
Intrasexual competition and sexual selection in cooperative mammals.Nature. 2006 Dec 21;444(7122):1065-8. doi: 10.1038/nature05386. Nature. 2006. PMID: 17183322
-
Female competition and aggression: interdisciplinary perspectives.Philos Trans R Soc Lond B Biol Sci. 2013 Oct 28;368(1631):20130073. doi: 10.1098/rstb.2013.0073. Print 2013. Philos Trans R Soc Lond B Biol Sci. 2013. PMID: 24167303 Free PMC article.
Cited by
-
Rapid juvenile hormone downregulation in subordinate wasp queens facilitates stable cooperation.Proc Biol Sci. 2018 Feb 14;285(1872):20172645. doi: 10.1098/rspb.2017.2645. Proc Biol Sci. 2018. PMID: 29436498 Free PMC article.
-
Elevated aggression is associated with uncertainty in a network of dog dominance interactions.Proc Biol Sci. 2019 Jul 10;286(1906):20190536. doi: 10.1098/rspb.2019.0536. Epub 2019 Jul 3. Proc Biol Sci. 2019. PMID: 31266423 Free PMC article.
-
Relatedness and spatial distance modulate intergroup interactions: experimental evidence from a social rodent.Curr Zool. 2019 Oct;65(5):527-534. doi: 10.1093/cz/zoy082. Epub 2018 Nov 16. Curr Zool. 2019. PMID: 31616483 Free PMC article.
-
Wake up and smell the conflict: odour signals in female competition.Philos Trans R Soc Lond B Biol Sci. 2013 Oct 28;368(1631):20130082. doi: 10.1098/rstb.2013.0082. Print 2013. Philos Trans R Soc Lond B Biol Sci. 2013. PMID: 24167312 Free PMC article. Review.
-
Female reproductive competition explains variation in prenatal investment in wild banded mongooses.Sci Rep. 2016 Jan 28;6:20013. doi: 10.1038/srep20013. Sci Rep. 2016. PMID: 26817515 Free PMC article.
References
-
- Vehrencamp SL. 1983. A model for the evolution of despotic versus egalitarian societies. Anim. Behav. 31, 667–682 (doi:10.1016/S0003-3472(83)80222-X) - DOI
-
- Johnstone RA. 2000. Models of reproductive skew: a review and synthesis (invited article). Ethology 106, 5–26 (doi:10.1046/j.1439-0310.2000.00529.x) - DOI
-
- Clutton-Brock TH. 1998. Reproductive skew, concessions and limited control. Trends Ecol. Evol. 13, 288–292 (doi:10.1016/S0169-5347(98)01402-5) - DOI - PubMed
-
- Keller L, Reeve HK. 1994. Partitioning of reproduction in animal societies. Trends Ecol. Evol. 9, 98–103 (doi:10.1016/0169-5347(94)90204-6) - DOI - PubMed
-
- Clutton-Brock T, Huchard E. 2013. Social competition and its consequences in female mammals. J. Zool. 289, 151–171 (doi:10.1111/jzo.12023) - DOI
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

