Interior-point methods for estimating seasonal parameters in discrete-time infectious disease models
- PMID: 24167542
- PMCID: PMC3805536
- DOI: 10.1371/journal.pone.0074208
Interior-point methods for estimating seasonal parameters in discrete-time infectious disease models
Abstract
Infectious diseases remain a significant health concern around the world. Mathematical modeling of these diseases can help us understand their dynamics and develop more effective control strategies. In this work, we show the capabilities of interior-point methods and nonlinear programming (NLP) formulations to efficiently estimate parameters in multiple discrete-time disease models using measles case count data from three cities. These models include multiplicative measurement noise and incorporate seasonality into multiple model parameters. Our results show that nearly identical patterns are estimated even when assuming seasonality in different model parameters, and that these patterns show strong correlation to school term holidays across very different social settings and holiday schedules. We show that interior-point methods provide a fast and flexible approach to parameterizing models that can be an alternative to more computationally intensive methods.
Conflict of interest statement
Figures
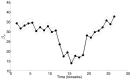

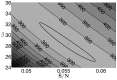
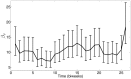
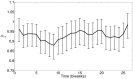
 used in the SIR simulation (circles).
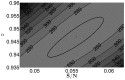
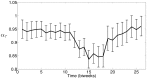
used in the SIR simulation (circles).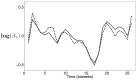
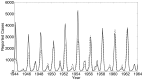

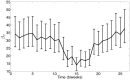


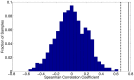

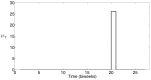
References
-
- Hethcote HW (2000) The mathematics of infectious diseases. SIAM Review 42: 599–653.
-
- Finkenstädt B, Bjornstad O, Grenfell B (2002) A stochastic model for extinction and recurrence of epidemics: estimation and inference for measles outbreaks. Biostatistics 3: 493–510. - PubMed
-
- Bjornstad ON, Finkenstädt B, Grenfell BT (2002) Dynamics of measles epidemics: Estimating Scaling of Transmission Rates Using a Time Series SIR Model. Ecological Monographs 72: 169–184.
-
- Fourer R, Gay DM, Kernighan BW (1993) AMPL: A Modeling Language for Mathematical Programming. Danvers, MA, USA: The Scientific Press (now an imprint of Boyd & Fraser Publishing Co.), xvi+351 pp.
-
- Rosenthal RE (2012) GAMS: A User's Guide GAMS Development Corporation.
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Medical

