Deriving quantitative dynamics information for proteins and RNAs using ROTDIF with a graphical user interface
- PMID: 24170368
- PMCID: PMC3939081
- DOI: 10.1007/s10858-013-9791-1
Deriving quantitative dynamics information for proteins and RNAs using ROTDIF with a graphical user interface
Abstract
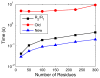
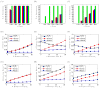
To facilitate rigorous analysis of molecular motions in proteins, DNA, and RNA, we present a new version of ROTDIF, a program for determining the overall rotational diffusion tensor from single- or multiple-field nuclear magnetic resonance relaxation data. We introduce four major features that expand the program's versatility and usability. The first feature is the ability to analyze, separately or together, (13)C and/or (15)N relaxation data collected at a single or multiple fields. A significant improvement in the accuracy compared to direct analysis of R2/R1 ratios, especially critical for analysis of (13)C relaxation data, is achieved by subtracting high-frequency contributions to relaxation rates. The second new feature is an improved method for computing the rotational diffusion tensor in the presence of biased errors, such as large conformational exchange contributions, that significantly enhances the accuracy of the computation. The third new feature is the integration of the domain alignment and docking module for relaxation-based structure determination of multi-domain systems. Finally, to improve accessibility to all the program features, we introduced a graphical user interface that simplifies and speeds up the analysis of the data. Written in Java, the new ROTDIF can run on virtually any computer platform. In addition, the new ROTDIF achieves an order of magnitude speedup over the previous version by implementing a more efficient deterministic minimization algorithm. We not only demonstrate the improvement in accuracy and speed of the new algorithm for synthetic and experimental (13)C and (15)N relaxation data for several proteins and nucleic acids, but also show that careful analysis required especially for characterizing RNA dynamics allowed us to uncover subtle conformational changes in RNA as a function of temperature that were opaque to previous analysis.
Figures
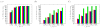

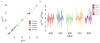


References
-
- Blackledge M, Cordier F, Dosset P, Marion D. Precision and uncertainty in the characterization of anisotropic rotational diffusion by 15N relaxation. Journal of the American Chemical Society. 1998;120(18):4538–4539.
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

