Exploiting imperfections in the bulk to direct assembly of surface colloids
- PMID: 24191037
- PMCID: PMC3839777
- DOI: 10.1073/pnas.1313551110
Exploiting imperfections in the bulk to direct assembly of surface colloids
Abstract
We exploit the long-ranged elastic fields inherent to confined nematic liquid crystals (LCs) to assemble colloidal particles trapped at the LC interface into reconfigurable structures with complex symmetries and packings. Spherical colloids with homeotropic anchoring trapped at the interface between air and the nematic LC 4-cyano-4'-pentylbiphenyl create quadrupolar distortions in the director field causing particles to repel and consequently form close-packed assemblies with a triangular habit. Here, we report on complex open structures organized via interactions with defects in the bulk. Specifically, by confining the nematic LC in an array of microposts with homeotropic anchoring conditions, we cause defect rings to form at well-defined locations in the bulk of the sample. These defects source elastic deformations that direct the assembly of the interfacially trapped colloids into ring-like assemblies, which recapitulate the defect geometry even when the microposts are completely immersed in the nematic. When the surface density of the colloids is high, they form a ring near the defect and a hexagonal lattice far from it. Because topographically complex substrates are easily fabricated and LC defects are readily reconfigured, this work lays the foundation for a versatile, robust mechanism to direct assembly dynamically over large areas by controlling surface anchoring and associated bulk defect structure.
Keywords: 2D superstructures; directed assembly; elastic interaction; nematic interface; topology.
Conflict of interest statement
The authors declare no conflict of interest.
Figures
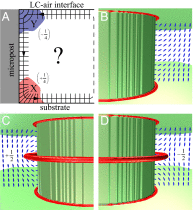
 are shown in red, where S is the leading eigenvalue of Q. Blue ellipsoids indicate the director field. The nematic is locally melted at the sharp corners. (B) Opposite winding at the two corners precludes the possibility of a disclination in the bulk. (C) Bulk disclination with
are shown in red, where S is the leading eigenvalue of Q. Blue ellipsoids indicate the director field. The nematic is locally melted at the sharp corners. (B) Opposite winding at the two corners precludes the possibility of a disclination in the bulk. (C) Bulk disclination with  (i.e., anticlockwise) winding number requires positive winding at both corners. (D) Bulk disclination with
(i.e., anticlockwise) winding number requires positive winding at both corners. (D) Bulk disclination with  (i.e., clockwise) winding number requires negative winding at both corners. Because the numerics show that the (meta)stable states have azimuthal symmetry and that the director has no azimuthal component, we may think of these winding numbers as pseudocharges.
(i.e., clockwise) winding number requires negative winding at both corners. Because the numerics show that the (meta)stable states have azimuthal symmetry and that the director has no azimuthal component, we may think of these winding numbers as pseudocharges.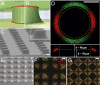

 . (B) Ring of colloids forms above a submerged micropost. (C) At moderate surface coverage, ordered rings assemble around the micropost due to attraction by the bulk defect and repel one another via long-range interparticle repulsion. As particle density continues to increase, radial assemblies evolve into hexagonal ordering (D) until highly ordered structures form at a very high surface coverage (E). (Scale bars: 50 μm.)
. (B) Ring of colloids forms above a submerged micropost. (C) At moderate surface coverage, ordered rings assemble around the micropost due to attraction by the bulk defect and repel one another via long-range interparticle repulsion. As particle density continues to increase, radial assemblies evolve into hexagonal ordering (D) until highly ordered structures form at a very high surface coverage (E). (Scale bars: 50 μm.)
 and follows
and follows  (solid curves), where
(solid curves), where  is the inferred elastic potential and r is the radial distance in the horizontal plane from the center of the micropost. As the height of a micropost is increased (different curves), attractions become weaker due to an increased separation between particles and the bulk defect. (Inset) Migration rates are faster for microposts with base curvature compared with those of comparable height that have a sharp corner at the base (corner Y in Fig. 2A). This is due to the tendency of the bulk disclination to position itself closer to the free interface for microposts with curved bases. Closed symbols indicate microposts with a curved base. (B) Numerically modeled energy of a colloidal sphere approaching a micropost capturing the
is the inferred elastic potential and r is the radial distance in the horizontal plane from the center of the micropost. As the height of a micropost is increased (different curves), attractions become weaker due to an increased separation between particles and the bulk defect. (Inset) Migration rates are faster for microposts with base curvature compared with those of comparable height that have a sharp corner at the base (corner Y in Fig. 2A). This is due to the tendency of the bulk disclination to position itself closer to the free interface for microposts with curved bases. Closed symbols indicate microposts with a curved base. (B) Numerically modeled energy of a colloidal sphere approaching a micropost capturing the  dependence of the quadrupolar colloid interacting with a disclination ring. The red dashed line represents the asymptotic value for
dependence of the quadrupolar colloid interacting with a disclination ring. The red dashed line represents the asymptotic value for  at large distances, and
at large distances, and  is the radius of the micropost’s disclination ring. (Inset) Representative image of the numerical modeling.
is the radius of the micropost’s disclination ring. (Inset) Representative image of the numerical modeling.References
-
- Wulff G. On the question of the rate of growth and dissolution of crystal surfaces. Z Kristallogr Miner. 1901;34:449–530.
-
- Thouless D, Kohmoto M, Nightingale M, Den Nijs M. Quantized Hall conductance in a two-dimensional periodic potential. Phys Rev Lett. 1982;49:405–408.
-
- Aharony O, Gubser SS, Maldacena J, Ooguri H, Oz Y. Large N field theories, string theory and gravity. Phys Rep. 2000;323:183–386.
-
- Price RR, et al. Quality assurance methods and phantoms for magnetic resonance imaging: Report of AAPM nuclear magnetic resonance Task Group No. 1. Med Phys. 1990;17(2):287–295. - PubMed
-
- Gharbi MA, et al. Behavior of colloidal particles at a nematic liquid crystal interface. Soft Matter. 2011;7:1467–1471.
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources
Other Literature Sources

