A microstructurally motivated model of arterial wall mechanics with mechanobiological implications

Abstract

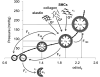
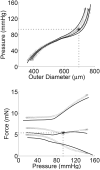
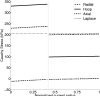
Through mechanobiological control of the extracellular matrix, and hence local stiffness, smooth muscle cells of the media and fibroblasts of the adventitia play important roles in arterial homeostasis, including adaptations to altered hemodynamics, injury, and disease. We present a new approach to model arterial wall mechanics that seeks to define better the mechanical environments of the media and adventitia while avoiding the common prescription of a traction-free reference configuration. Specifically, we employ the concept of constituent-specific deposition stretches from the growth and remodeling literature and define a homeostatic state at physiologic pressure and axial stretch that serves as a convenient biologically and clinically relevant reference configuration. Information from histology and multiphoton imaging is then used to prescribe structurally motivated constitutive relations for a bi-layered model of the wall. The utility of this approach is demonstrated by describing in vitro measured biaxial pressure-diameter and axial force-length responses of murine carotid arteries and predicting the associated intact and radially cut traction-free configurations. The latter provides a unique validation while confirming that this constrained mixture approach naturally recovers estimates of residual stresses, which are fundamental to wall mechanics, without the usual need to prescribe an opening angle that is only defined conveniently on cylindrical geometries and cannot be measured in vivo. Among other findings, the model suggests that medial and adventitial stresses can be nearly uniform at physiologic loads, albeit at separate levels, and that the adventitia bears increasingly more load at supra-physiologic pressures while protecting the media from excessive stresses.

FIGURE 1

Schematic illustration of some of the key configurations that were used in the nonlinear regression or used to test the predictive ability of the constitutive formulation for the mouse carotid artery. κ_h: homeostatic configuration at a mean arterial pressure of 93 mmHg and in vivo axial stretch ${\lambda }_z^{iv}=1.5$ to 1.6. κ_p: loaded configurations at ${\lambda }_z^{iv}$ and any pressure P, with representative values shown for P = 0, 60, 180 mmHg. κ_tf: intact, traction-free configuration. κ_c: radially cut, traction-free configuration. κ_n: natural (i.e., stress-free) configurations for individual constituents. All configurations are shown on a graph where the transmural pressure is plotted against the current outer diameter (od) as predicted by the numerical model, relative to the outer diameter in the intact, traction-free configuration κ_tf. Note, for example, that the κ₀ configuration is unpressurized but axially stretched, hence its diameter is less than that in the intact traction-free configuration.

FIGURE 2

Illustrative cross-sections from a wild-type mouse carotid artery stained with Verhoeff-Van Gieson (VVG, top, left) and Masson’s Tri-Chrome (MTC, top, right) and imaged at 20x magnification. The bottom masks separate the primary load-bearing constituents based on the hue, saturation and lightness (HSL) values pertaining to each pixel. In addition to the usual observations (e.g., that elastin and smooth muscle are confined primarily to the media and the adventitia consists mainly of dense collagen), note the thin layers of collagen that adjoin the elastic laminae in the media.

FIGURE 3

Representative best-fit (solid symbols / lines) to pressure vs. outer diameter and axial force vs. pressure data (open symbols) collected during cyclic pressure-diameter testing at three different axial stretches, ${\lambda }_z^{iv}$ and ${\lambda }_z^{iv}\pm 5\%$, for one of the three arteries tested. This fit was obtained using the constitutive relationship in Eq. (13) and objective function in Eq. (19). The symbol * shows the selected in-vivo, homeostatic state (P ~ 93 mmHg and ${\lambda }_z^{iv}\sim 1.55$). Note that the predictions in the pressure – diameter plot reveal a slight change in slope (between 60 and 80 mmHg), which signals the assumed transition from possible compression and tension in the collagen fibers to tension only in these fibers (cf. Table 3).

FIGURE 4

Representative iso-energy contour plots of W in the plane λ_θ – λ_z for the media (upper panel) and the adventitia (lower panel), with the ranges of stretch chosen to cover all deformations that were included in the stress analyses. In contrast with most formulations, note that the reference configuration is the in vivo homeostatic configuration, with components of F given by (λ_θ, λ_z) = (1,1) as indicated by the *. This plot confirms that the media bears most of the load in the homeostatic configuration and shows the different anisotropies in the media and adventitia based on our best-fit values of the material parameters. Finally, these contours confirm convexity of W even in compression; the superimposed numerical values on the contours denote the values of strain energy in kPa.

FIGURE 5

Predicted transmural distributions of radial (dash-dotted), circumferential (solid), and axial (dashed) components of Cauchy stress in the homeostatic configuration κ_h, at mean arterial pressure (MAP ~ 93 mmHg) and ${\lambda }_z^{iv}=1.5$, based on one representative set of estimated parameters. The mean circumferential stress, as obtained from Laplace’s relation, is shown for comparison (dotted horizontal line). All components of stress are plotted as a function of the normalized current radius, with 0 and 1 corresponding to inner and outer radii, respectively. The vertical light grey solid line identifies the border between the media and adventitia, at approximately 0.42.

FIGURE 6

Representative transmural distributions of components of the extra stress t̄ for the elastic network, collagen fibers, and smooth muscle plus associated circumferential (c) collagen fibers, all for three different loading configurations. Upper panel: intact, traction-free configuration κ_tf. Middle panel: homeostatic configuration κ_h at mean arterial pressure and ${\lambda }_z^{iv}$. Lower panel: elevated pressure configuration κ₁₈₀ at 180 mmHg and ${\lambda }_z^{iv}$. Similar to Figure 5, stress is plotted as a function of the normalized radius ∈ [0,1]. The vertical light grey solid line that locates the interface between the media and adventitia falls approximately at 0.45 in κ_tf and at 0.42 in both κ_h and κ₁₈₀.

FIGURE 7

Representative transmural distribution of Cauchy stress in the circumferential direction for four different pressures above homeostatic: 100 mmHg (dash-dotted line), 140 mmHg (dotted line), 180 mmHg (solid line), and 220 mmHg (dashed line). Similar to Fig. 5, stress is plotted as a function of the normalized radius ∈ [0,1]. The media/adventitia boundary occurs approximately at 0.42. Note the much more dramatic increase in adventitial stress.