Convergence and rate analysis of neural networks for sparse approximation
- PMID: 24199030
- PMCID: PMC3816963
- DOI: 10.1109/TNNLS.2012.2202400
Convergence and rate analysis of neural networks for sparse approximation
Erratum in
- IEEE Trans Neural Netw Learn Syst. 2014 Aug;25(8):1595-6
Abstract
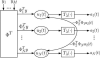
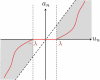
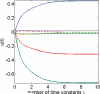
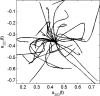
We present an analysis of the Locally Competitive Algorithm (LCA), which is a Hopfield-style neural network that efficiently solves sparse approximation problems (e.g., approximating a vector from a dictionary using just a few nonzero coefficients). This class of problems plays a significant role in both theories of neural coding and applications in signal processing. However, the LCA lacks analysis of its convergence properties, and previous results on neural networks for nonsmooth optimization do not apply to the specifics of the LCA architecture. We show that the LCA has desirable convergence properties, such as stability and global convergence to the optimum of the objective function when it is unique. Under some mild conditions, the support of the solution is also proven to be reached in finite time. Furthermore, some restrictions on the problem specifics allow us to characterize the convergence rate of the system by showing that the LCA converges exponentially fast with an analytically bounded convergence rate. We support our analysis with several illustrative simulations.
Figures



Similar articles
-
Subgradient-based neural networks for nonsmooth nonconvex optimization problems.IEEE Trans Neural Netw. 2009 Jun;20(6):1024-38. doi: 10.1109/TNN.2009.2016340. Epub 2009 May 19. IEEE Trans Neural Netw. 2009. PMID: 19457749
-
A smooth gradient approximation neural network for general constrained nonsmooth nonconvex optimization problems.Neural Netw. 2025 Apr;184:107121. doi: 10.1016/j.neunet.2024.107121. Epub 2025 Jan 6. Neural Netw. 2025. PMID: 39798354
-
Convergence analysis of a deterministic discrete time system of Oja's PCA learning algorithm.IEEE Trans Neural Netw. 2005 Nov;16(6):1318-28. doi: 10.1109/TNN.2005.852236. IEEE Trans Neural Netw. 2005. PMID: 16342477
-
Fast sparse approximation for least squares support vector machine.IEEE Trans Neural Netw. 2007 May;18(3):685-97. doi: 10.1109/TNN.2006.889500. IEEE Trans Neural Netw. 2007. PMID: 17526336
-
Optimal sparse approximation with integrate and fire neurons.Int J Neural Syst. 2014 Aug;24(5):1440001. doi: 10.1142/S0129065714400012. Epub 2014 Mar 23. Int J Neural Syst. 2014. PMID: 24875786
Cited by
-
A compressed sensing perspective of hippocampal function.Front Syst Neurosci. 2014 Aug 8;8:141. doi: 10.3389/fnsys.2014.00141. eCollection 2014. Front Syst Neurosci. 2014. PMID: 25152718 Free PMC article.
-
A common network architecture efficiently implements a variety of sparsity-based inference problems.Neural Comput. 2012 Dec;24(12):3317-39. doi: 10.1162/NECO_a_00372. Epub 2012 Sep 12. Neural Comput. 2012. PMID: 22970876 Free PMC article.
-
Sparse Coding Using the Locally Competitive Algorithm on the TrueNorth Neurosynaptic System.Front Neurosci. 2019 Jul 23;13:754. doi: 10.3389/fnins.2019.00754. eCollection 2019. Front Neurosci. 2019. PMID: 31396039 Free PMC article.
-
Constrained brain volume in an efficient coding model explains the fraction of excitatory and inhibitory neurons in sensory cortices.PLoS Comput Biol. 2022 Jan 21;18(1):e1009642. doi: 10.1371/journal.pcbi.1009642. eCollection 2022 Jan. PLoS Comput Biol. 2022. PMID: 35061666 Free PMC article.
-
Visual nonclassical receptive field effects emerge from sparse coding in a dynamical system.PLoS Comput Biol. 2013;9(8):e1003191. doi: 10.1371/journal.pcbi.1003191. Epub 2013 Aug 29. PLoS Comput Biol. 2013. PMID: 24009491 Free PMC article.
References
-
- Balavoine A, Rozell CJ, Romberg J. Global convergence of the locally competitive algorithm. Proc. IEEE Digital Signal Process. Workshop. 2011 Jan;:431–436.
-
- Elad M, Figueiredo MAT, Ma Y. On the role of sparse and redundant representations in image processing. Proc. IEEE. 2010 Jun;98(6):972–982.
-
- Olshausen BA, Field DJ. Sparse coding of sensory inputs. Current Opinion Neurobiol. 2004 Aug;14(4):481–487. - PubMed
-
- Olshausen BA, Field DJ. Emergence of simple-cell receptive field properties by learning a sparse code for natural images. Nature. 1996 Jun.381(6583):607–609. - PubMed
-
- Olshausen BA, Field DJ. Sparse coding with an overcomplete basis set: A strategy employed by V1? Vis. Res. 1997 Dec.37(23):3311–3325. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Research Materials

