Convergence and rate analysis of neural networks for sparse approximation

Abstract

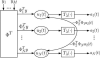
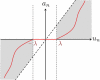
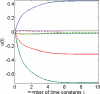
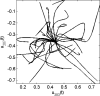
We present an analysis of the Locally Competitive Algorithm (LCA), which is a Hopfield-style neural network that efficiently solves sparse approximation problems (e.g., approximating a vector from a dictionary using just a few nonzero coefficients). This class of problems plays a significant role in both theories of neural coding and applications in signal processing. However, the LCA lacks analysis of its convergence properties, and previous results on neural networks for nonsmooth optimization do not apply to the specifics of the LCA architecture. We show that the LCA has desirable convergence properties, such as stability and global convergence to the optimum of the objective function when it is unique. Under some mild conditions, the support of the solution is also proven to be reached in finite time. Furthermore, some restrictions on the problem specifics allow us to characterize the convergence rate of the system by showing that the LCA converges exponentially fast with an analytically bounded convergence rate. We support our analysis with several illustrative simulations.

Fig. 1

Block diagram of the LCA [14], which is a Hopfield-style network architecture for solving sparse approximation problems.

Fig. 2

Soft-thresholding activation function. When this is used for the thresholding function T_λ(·), the LCA solves the popular BPDN optimization problem used in many sparse approximation applications.

Fig. 3

Generic activation function satisfying conditions (6). The area in gray represents where the activation function must lie in order to satisfy conditions (6b) and (6c).

Fig. 4

Plot of the evolution with respect to time of several LCA nodes u_k(t). The plain lines correspond to nodes that are active in the final solution and the dashed lines correspond to nodes that are inactive in the final solution.

Fig. 5

Output a* of the LCA after convergence. Only nonzero elements are plotted. The fixed point reached by the system is very close to the initial sparse vector used to create the measurement vector (it cannot be exact due to noise). The solution is also very close to a standard digital solver [8] run using the same inputs. Note that the LCA produces many coefficients that are exactly zero (therefore not plotted).

Fig. 6

Trajectories of u(t) in the plane defined by two nodes chosen randomly from the active set. Trajectories are shown for 30 random initial states.

Fig. 7

Histogram (in percentage) of the number of switches the LCA requires before convergence over 1000 trials.

Fig. 8

Convergence behavior of $(1∕2){\Vert u\left(t\right)-u^{\ast }\Vert }_2^2$. The dashed line shows the theoretical decay in (20) with δ* computed by using the final solution support. The dash-dot line shows the theoretical decay with δ_max computed on the largest support visited. While both estimates are showing theoretically correct behavior, the estimate of the rate based on δ* is more empirically accurate than the conservative estimate based on δ_max.