Folding behaviour of Tachi-Miura polyhedron bellows
- PMID: 24204186
- PMCID: PMC3780822
- DOI: 10.1098/rspa.2013.0351
Folding behaviour of Tachi-Miura polyhedron bellows
Abstract
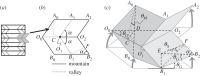
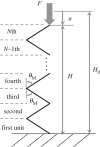
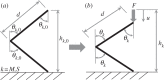
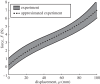
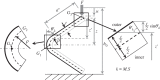
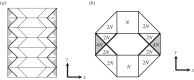
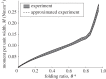
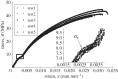
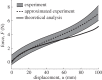
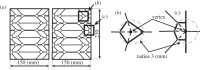
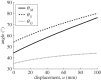
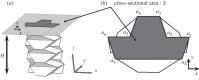
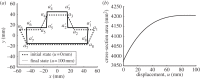
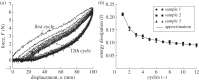
In this paper, we examine the folding behaviour of Tachi-Miura polyhedron (TMP) bellows made of paper, which is known as a rigid-foldable structure, and construct a theoretical model to predict the mechanical energy associated with the compression of TMP bellows, which is compared with the experimentally measured energy, resulting in the gap between the mechanical work by the compression force and the bending energy distributed along all the crease lines. The extended Hamilton's principle is applied to explain the gap which is considered to be energy dissipation in the mechanical behaviour of TMP bellows.
Keywords: Miura-ori; Tachi–Miura polyhedron; energy dissipation; extended Hamilton's principle; origami.
Figures




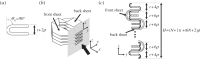
References
-
- Guest SD, Pellegrino S. 1994. The folding of triangulated cylinders, part I: geometric considerations. J. Appl. Mech. 61, 773–777 (doi:10.1115/1.2901553) - DOI
-
- Guest SD, Pellegrino S. 1996. The folding of triangulated cylinders, part III: experiments. J. Appl. Mech. 63, 77–83 (doi:10.1115/1.2787212) - DOI
-
- Hunt GW, Ario I. 2005. Twist buckling and the foldable cylinder: an exercise in origami. Int. J. Non-Linear Mech. 40, 833–843 (doi:10.1016/j.ijnonlinmec.2004.08.011) - DOI
-
- Yoshimura Y. 1955. On the mechanism of buckling of a circular cylindrical shell under axial compression, NACA TM 1390.
-
- Ario I, Nakazawa M. 2010. Non-linear dynamic behavior of multi-folding microstructure systems based on origami skill. Int. J. Non-Linear Mech. 45, 337–347 (doi:10.1016/j.ijnonlinmec.2009.11.010) - DOI
LinkOut - more resources
Full Text Sources
Other Literature Sources
Miscellaneous

