Transient dynamics of an elastic capsule in a microfluidic constriction

Abstract

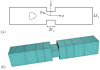
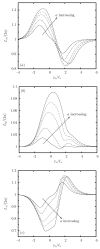
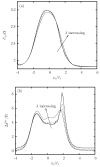
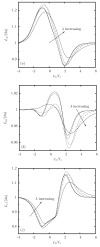
In this paper we investigate computationally the transient dynamics of an elastic capsule flowing in a square microchannel with a rectangular constriction, and compare it with that of a droplet. The confinement and expansion dynamics of the fluid flow results in a rich deformation behavior for the capsule, from an elongated shape at the constriction entrance, to a flattened parachute shape at its exit. Larger capsules are shown to take more time to pass the constriction and cause higher additional pressure difference, owing to higher flow blocking. Our work highlights the effects of two different mechanisms for non-tank-treading transient capsule dynamics. The capsule deformation results from the combined effects of the surrounding and inner fluids' normal stresses on the soft particle's interface, and thus when the capsule viscosity increases, its transient deformation decreases, as for droplets. However, the capsule deformation is not able to create a strong enough inner circulation (owing to restrictions imposed by the material membrane), and thus the viscosity ratio does not affect much the capsule velocity and the additional pressure difference. In addition, the weak inner circulation results in a positive additional pressure difference ΔP⁺ even for low-viscosity capsules, in direct contrast to low-viscosity droplets which create a negative ΔP⁺. Our findings suggest that the high cytoplasmatic viscosity, owing to the protein hemoglobin required for oxygen transport, does not affect adversely the motion of non-tank-trading erythrocytes in vascular capillaries.

FIG. 1

(a) Illustration of an elastic capsule flowing at the centerline of a square microchannel with a rectangular constriction. (b) Spectral boundary element discretization of the microfluidic geometry.

FIG. 2

The shape of a Skalak capsule with C = 1, a/ℓ_z = 1, λ = 1 and Ca = 0.1 moving inside the microfluidic constriction. The capsule’s centroid x_c/ℓ_z is (a) −1.51, (b) −0.1, (c) 0.81, and (d) 2.05. The three-dimensional capsule views were derived from the actual spectral grid using orthographic projection in plotting.

FIG. 3

Evolution of the capsule lengths as a function of the centroid x_c, for a Skalak capsule with C = 1, Ca = 0.1 and λ = 1, for size a/ℓ_z = 0.4, 0.6, 0.8, 0.9, 1. (a) Length L_x, (b) width L_y, and (c) height L_z (scaled with the length 2a of the undisturbed spherical shape). These lengths are determined as the maximum distance of the interface in the x, y and z directions.

FIG. 4

The shape of a Skalak capsule with C = 1, a/ℓ_z = 1, λ = 1 and Ca = 0.1 moving inside the microfluidic constriction for capsule’s centroid (a) x_c/ℓ_z = −1.51 and (b) x_c/ℓ_z = 2.05. The capsule shape is plotted as seen slightly askew from the positive z-axis to reveal its fully three-dimensional conformation.

FIG. 5

Evolution of (a) the capsule velocity U_x, and (b) the additional pressure difference ΔP⁺, as a function of the centroid x_c, for a Skalak capsule with C = 1, Ca = 0.1 and λ = 1, for size a/ℓ_z = 0.4, 0.6, 0.8, 0.9, 1.

FIG. 6

Evolution of the capsule lengths as a function of the centroid x_c, for a Skalak capsule with C = 1, a/ℓ_z = 0.9 and Ca = 0.1, for viscosity ratio λ = 0.01, 0.1, 1, 2, 5. (a) Length L_x, (b) width L_y, and (c) height L_z (scaled with the length 2a of the undisturbed spherical shape). Our results for λ = 0.01 are identical for lower viscosity ratios, e.g. λ = 0.001, 0, and thus represent the low-viscosity limit λ << 1.

FIG. 7

Evolution of (a) the capsule velocity U_x, and (b) the additional pressure difference ΔP⁺, as a function of the centroid x_c, for a Skalak capsule with C = 1, a/ℓ_z = 0.9 and Ca = 0.1, for viscosity ratio λ = 0.01, 0.1, 1, 2, 5.

FIG. 8

Evolution of the droplet lengths as a function of the centroid x_c, for a droplet with a/ℓ_z = 0.9, Ca = 0.1 and viscosity ratio λ = 0.01, 0.1, 1, 2, 5. (a) Length L_x, (b) width L_y, and (c) height L_z (scaled with the length 2a of the undisturbed spherical shape). Our results for λ = 0.01 are identical for lower viscosity ratios, e.g. λ = 0.001, 0, and thus represent the low-viscosity limit λ << 1.

FIG. 9

Evolution of (a) the velocity U_x, and (b) the additional pressure difference ΔP⁺, as a function of the centroid x_c, for a droplet with a/ℓ_z = 0.9, Ca = 0.1 and viscosity ratio λ = 0.01, 0.1, 1, 2, 5.