A mathematical framework for the registration and analysis of multi-fascicle models for population studies of the brain microstructure

Abstract

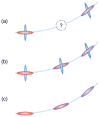
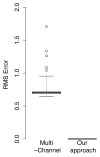
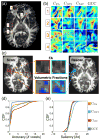
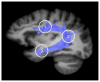
Diffusion tensor imaging (DTI) is unable to represent the diffusion signal arising from multiple crossing fascicles and freely diffusing water molecules. Generative models of the diffusion signal, such as multi-fascicle models, overcome this limitation by providing a parametric representation for the signal contribution of each population of water molecules. These models are of great interest in population studies to characterize and compare the brain microstructural properties. Central to population studies is the construction of an atlas and the registration of all subjects to it. However, the appropriate definition of registration and atlasing methods for multi-fascicle models have proven challenging. This paper proposes a mathematical framework to register and analyze multi-fascicle models. Specifically, we define novel operators to achieve interpolation, smoothing and averaging of multi-fascicle models. We also define a novel similarity metric to spatially align multi-fascicle models. Our framework enables simultaneous comparisons of different microstructural properties that are confounded in conventional DTI. The framework is validated on multi-fascicle models from 24 healthy subjects and 38 patients with tuberous sclerosis complex, 10 of whom have autism. We demonstrate the use of the multi-fascicle models registration and analysis framework in a population study of autism spectrum disorder.

Fig. 1

Computing weighted combinations of multi-fascicle models amounts to computing the complete mixture and simplifying it in an EM scheme to obtain . The E-step is a clustering problem and the M-step consists in averaging log-tensors in each cluster.

Fig. 2

Single-tensor and multi-fascicle atlases overlaid on the T1-weighted MRI atlas. The multi-fascicle atlas presents tensors with higher fractional anisotropies than the single-tensor atlas. This is due to the account of both the free water diffusion in the isotropic compartment and the multiple fascicle present in the voxel. The highlighted regions represent the corona radiata where projections of the corpus callosum cross cortico-spinal tracts, and a region where the pyramidal tracts (vertical lines) and the medial cerebellar peduncle (horizontal lines) cross.

Fig. 3

Fascicle-based spatial statistics (FBSS) proceeds in three steps. (a) Fascicles (grey line) are drawn on the atlas with a sub-voxel resolution. The point in the middle is at a non-grid location. (b) Multi-fascicle models are interpolated at non-grid locations. (c) At each location along the fascicle, the tensor most aligned to the fascicle is selected to compute the property of interest (FA, MD, etc.).

Fig. 4

Average RMS error of the deformation fields obtained by registering a multi-fascicle model with itself after randomly relabeling tensors. Our framework is invariant under relabeling leading to an error that is exactly zero. By contrast, multi-channel registration yields non-zero deformation fields.

Fig. 5

Estimation of the interpolation errors demonstrates the superiority of the proposed approach compared to the multi-channel alternative to compute linear combinations of multi-fascicle models. The bar plots show the interpolation error for four metrics (Δ_FA, Δ_MD, Fro and Δ_Dir) under three different transformations.

Fig. 6

(Left) Performing interpolation for each tensor independently (considered as channels of a multi-channel image) confounds fascicles resulting in an inflated result. (Right) Weighted combination of multi-fascicle models introduced in our mathematical framework clusters similar fascicles to avoid the inflation effect. (a–b) Results obtained on synthetic data by interpolating the multi-fascicle models at the extremities. (c–d) Results obtained on in vivo data by applying a linear transform to a multi-fascicle model.

Fig. 7

The GCC for multi-fascicle models outperforms other metrics in terms of registration accuracy, as assessed by a scan-rescan experiment. (a) 495 regularly spaced landmarks are used for the experiment. (b) Similarity maps in four neighborhoods (circles indicate true matches) showing that GCC is the most specific metric. (c) In regions with no contrast in FA, the GCC is able to find correct matches due to robust patterns observed in multi-fascicle models. (d) The accuracy of the GCC is significantly better than all other metrics as seen by the cumulative distribution function (CDF). (e) No significant difference in saliency between the metrics are observed, except for a significantly higher saliency with C_DTI.

Fig. 8

Registering multi-fascicle models with our framework leads to higher alignment accuracies than registering single-tensor DTI with DTI-TK. (a) Quantitative assessment shows that registration errors using our framework are significantly lower than those obtained with DTI-TK [25]. (b) The difference in registration error is mostly visible in areas with crossing fascicles, where single-tensor DTI models have low contrast compared to multi-fascicle models. The zoomed-in areas are located in the corona radiata.

Fig. 9

Our mathematical framework leads to higher registration accuracies than the multi-channel alternative: the RMS errors (top) and its variance (bottom) are significantly lower. Results are shown for 1,440 registrations performed at various SNR for synthetic deformation fields (* p < 0.05, ** p < 0.005, *** p < 0.001).

Fig. 10

Morphometry results show areas with a significant volume deficit within the grey and white matter of TSC patients. (a) Multi-fascicle registration and multi-channel registration reveal more differences than single-tensor and the T1-weighted registrations. The differences observed with multi-fascicle registration are more consistent with the known anatomy than those observed with multi-channel registration, as seen for example in the left and right internal capsules.

Fig. 11

The dorsal language circuit is composed of white matter fascicles thought to connect Broca’s area in the frontal lobe (Region 1), Geschwind’s territory in the parietal lobe (Region 2), and Wernicke’s area in the temporal lobe (Region 3). The median tract was manually selected from those tracts to perform fascicle-based spatial statistics (FBSS).

Fig. 12

Fascicle-based spatial statistics of multi-fascicle models reveal local differences in the white fascicle properties that single tensor DTI cannot. Curves show the mean FA along the median tract of the dorsal language circuit in each group. Shaded area along the curves represent two standard errors. Grey rectangles indicate that the FA in that cluster is significantly different between the two groups. The top row studies differences between patients with tuberous sclerosis complex (TSC) and healthy controls. The bottom row further investigates differences between TSC patients with (TSC+ASD) and without autism (TSC-ASD). Landmarks 1, 2 and 3 correspond to those in Fig. 11.

Fig. 13

Multi-fascicle models reveal clusters of increased isotropic fraction in autism, potentially indicating the presence of neuroinflammation. Clusters found with our framework (top) are larger and more coherent than those obtained with the multi-channel alternative (results shown for t₀=3).