Coarse-grained model for colloidal protein interactions, B(22), and protein cluster formation

Abstract

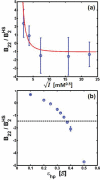
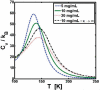
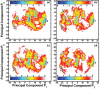
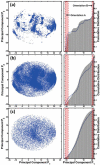
Reversible protein cluster formation is an important initial step in the processes of native and non-native protein aggregation, but involves relatively long time and length scales for detailed atomistic simulations and extensive mapping of free energy landscapes. A coarse-grained (CG) model is presented to semiquantitatively characterize the thermodynamics and key configurations involved in the landscape for protein oligomerization, as well as experimental measures of interactions such as the osmotic second virial coefficient (B22). Based on earlier work (Grüenberger et al., J. Phys. Chem. B 2013, 117, 763), this CG model treats proteins as rigid bodies composed of one bead per amino acid, with each amino acid having specific parameters for its size, hydrophobicity, and charge. The net interactions are a combination of steric repulsions, short-range attractions, and screened long-range charge-charge interactions. Model parametrization was done by fitting simulation results against experimental value of B22 as a function of solution ionic strength for α-chymotrypsinogen A and γD-Crystallin (gD-Crys). The CG model is applied to characterize the pairwise interactions and dimerization of gD-Crys and the dependence on temperature, protein concentration, and ionic strength. The results illustrate that at experimentally relevant conditions where stable dimers do not form, the entropic contributions are predominant in the free-energy of protein cluster formation and colloidal protein interactions, arguing against interpretations that treat B22 primarily from energetic considerations alone. Additionally, the results suggest that electrostatic interactions help to modulate the population of the different stable configurations for protein nearest-neighbor pairs, while short-range attractions determine the relative orientations of proteins within these configurations. Finally, simulation results are combined with Principal Component Analysis to identify those amino-acids/surface patches that form interprotein contacts at conditions that favor dimerization of gD-Crys. The resulting regions agree with previously found aggregation-prone sites, as well as suggesting new ones that may be important.

Figure 1

Comparison of experimental and calculated B₂₂ values for γD-crystallin at T = 300 K: (a) Theoretical (solid line) and experimental (symbols) B₂₂ as a function of the square root of the ionic strength. Theoretical B₂₂ curve is calculated for a value of ε_hp = 0.375$\mathcal{E}$ and ε_cc = 0.125$\mathcal{E}$. κ is assumed proportional to $\sqrt{I}$, with a proportionality constant α = 3.5 ± 0.5 M^−1/2nm⁻¹ obtained from fitting the resulting response surface of B₂₂ to the experimental data. See main text for additional details. (b) B₂₂ calculated via Mayer Sampling (symbols) as a function of ε_hp at high ionic strength (i.e., κ → 0, and/or ε_cc = 0). The horizontal dashed line corresponds to the experimental result determined via light scattering for an ionic strength of 504.2 mM. Values of B₂₂ are relative to the hard-sphere second virial coefficient $B_2^{HS}$ for a protein diameter of 4 nm.

Figure 2

Response surface for B₂₂ as function of screening length parameter κ and the electrostatic interactions parameter ε_cc. Symbols correspond to the values calculated via Mayer sampling for a value of ε_hp = 0.375 $\mathcal{E}$. The response surface is obtained by fitting the calculated B₂₂ values to a full-quadratic polynomial in 1/κ and ε_cc/ε_hp -i.e., including cross-terms. Details about the response surface and its fitted parameters are provided in the Supporting Information.

Figure 3

Comparison of theoretical and experimental osmotic second virial coefficient for α-chymotrypsinogen as a function of ionic strength I at T = 300 K. Theoretical B₂₂ curves correspond to: (solid line) B₂₂ response surface and (triangles) Mayer Sampling simulations. The response surface was calculated as a function of κ and ε_hp/ε_cc for ε_hp/ε_cc = 3, ε_hp = 4.08$\mathcal{E}$, and $\kappa ={\alpha }_{\mathrm{aCgn}}\sqrt{I}$, with α_aCgn = 3.08 ± 0.1 M^−1/2nm⁻¹ obtained from fitting the response surface to the experimental data (see Supporting Information). B₂₂ values from Mayer Sampling were calculated using the same values of the adjustable parameters obtained for gD-Crys (i.e., ε_hp = 0.375$\mathcal{E}$, ε_cc = 0.125$\mathcal{E}$, and α = 3.5 M^−1/2nm⁻¹). Other symbols correspond to experimental B₂₂ values published elsewhere for: (circles) pH=3.5 in 10mM citrate buffer and NaCl concentration between 0 and 100 mM; and (stars) pH=3 and I = 300 mM. Although the experimental value of B₂₂ at I = 300 mM was measured at pH=3, Velev et al. showed that B₂₂ is pH-independent for aCgn at that ionic strength. Inset provides the same data with I in a logarithmic scale.

Figure 4

Potential of mean force F (panel a and b), entropy S (panel c and d), and average interaction energy U (insets) curves as a function of the protein center-to-center distance r. Curves are shown at T = 100 (circles), 150 (squares), 200 (triangles), and 300 K (diamonds) for two different working cases: (first column) low ionic strength (1/κ = 40$\mathcal{L}$); and (second column) high ionic strength (1/κ = 0$\mathcal{L}$). 95% confidence intervals for all the values shown here are smaller than 0.05$\mathcal{E}$, and are not visible at the scale of the plots.

Figure 5

Two-dimensional free energy surfaces as a function of the electrostatic (E_cc) or van der Waals (E_vdw) energies and the center-to-center distance r for γD-crystallin at a protein concentration of 10 mg/mL and T = 100 (top row), 150 (middle row), and 300 K (bottom row). First and second columns correspond to simulation at large screening length (1/κ = 40 $\mathcal{L}$); third column provides the free energy surface for the case when electrostatic interactions are completely screened (1/κ = 0). Colors indicates free-energy values in units of $\mathcal{E}$, and its scale is shown next to each panel. With the exception of the left-most panel in the middle row, all color scales are the same for each panel.

Figure 6

Heat capacity C_v vs. T for all the simulations tested here: (dashed line) c = 5 mg/mL and 1/κ = 40 $\mathcal{L}$; (solid line) c = 10 mg/mL and 1/κ = 40 $\mathcal{L}$; (dotted line) c = 20 mg/mL and 1/κ = 40 $\mathcal{L}$; and (dash-dot line) c = 10 mg/mL and 1/κ = 0 $\mathcal{L}$.

Figure 7

Two-dimensional contour maps for the negative base-10-logarithm of the probability distribution function of the number of configurations as a function of the principal components P₁ and P₂ for γD-crystallin at T = 80 K. Each of the panels corresponds to one of the working cases: (a) c = 5mg/mL and 1/κ = 40$\mathcal{L}$; (b) c = 10mg/mL and 1/κ = 40$\mathcal{L}$; (c) c = 20mg/mL and 1/κ = 40$\mathcal{L}$; and (d) c = 10mg/mL and 1/κ = 0$\mathcal{L}$. Colors indicate the order of magnitude of the probability distribution function. The selected configurations for further analysis (A, B, and C) are labeled in each of the panels.

Figure 8

P₁ versus P₂ for the relevant configurations for the calculation of B₂₂ for γD-crystallin at 1/κ = 40 $\mathcal{L}$ and T = 100 (a), 150 (b), and 250 K (c). Rightmost panels next to each of (a), (b) and (c) compare the cumulative distribution function of P₁ obtained from the B₂₂ calculations (gray vertical bars) with that obtained from applying WHAM to the REMD simulation for c = 10 mg/mL and 1/κ = 40 $\mathcal{L}$ at the same temperatures (solid blue curve). The range of P₁ values corresponding to the two most populated configurations (orientations A and B) are also highlighted with red shaded regions on the cumulative distribution function in the righthand panels.

Figure 9

Self-association-prone sites (i.e., “hot-spot” residues) on γD-crystallin found from REMD simulations for the selected protein relative orientations: A, B, and C. Identity of the “hot-spot” residues are shown in panel (a), while panel (b) provides an schematic representation of these sites along the protein crystal structure. Note that the identified “hot-spot” residues agree with those obtained in a previous work based on a consensus among different aggregation predictors. Self-association-prone sites are shown as green beads in the figure. An alternative representation of the same information contained in panels (a) and (b) is provided in the form of illustrative snapshots of the low-temperature structures for the dimeric configurations A, B, and C in Figure S10 in the Supporting Information.