A maximum entropy framework for nonexponential distributions

Abstract

Probability distributions having power-law tails are observed in a broad range of social, economic, and biological systems. We describe here a potentially useful common framework. We derive distribution functions for situations in which a "joiner particle" k pays some form of price to enter a community of size , where costs are subject to economies of scale. Maximizing the Boltzmann-Gibbs-Shannon entropy subject to this energy-like constraint predicts a distribution having a power-law tail; it reduces to the Boltzmann distribution in the absence of economies of scale. We show that the predicted function gives excellent fits to 13 different distribution functions, ranging from friendship links in social networks, to protein-protein interactions, to the severity of terrorist attacks. This approach may give useful insights into when to expect power-law distributions in the natural and social sciences.

Keywords: fat tail; heavy tail; social physics; statistical mechanics; thermostatistics.

Fig. 1.

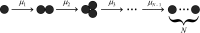
The joining cost for a particle to join a size community is . This diagram can describe particles forming colloidal clusters, or social processes such as people joining cities, citations added to papers, or link creation in a social network.

Fig. 2.

Eq. 7 gives good fits (; see SI Text for details) to 13 empirical distributions, with the values of and given in Table 1. Points are empirical data, and lines represent best-fit distributions. The probability of exactly k is shown in blue, and the probability of at least k (the complementary cumulative distribution, ) is shown in red. Descriptions and references for these datasets can be found in SI Text.

Fig. 3.

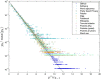
Eq. 7 fitted to the 13 datasets in Table 1, plotted against the total cost to assemble a size k community, . Values of and are shown in Table 1. The y axis has been rescaled by dividing by the maximum , so that all curves begin at . All data sets are fit by the line. See Fig. 2 for fits to individual datasets.