Mechanisms of scaling in pattern formation
- PMID: 24301464
- PMCID: PMC3848184
- DOI: 10.1242/dev.100511
Mechanisms of scaling in pattern formation
Abstract
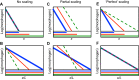
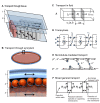
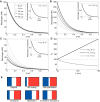
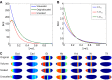
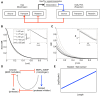
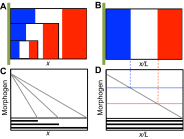
Many organisms and their constituent tissues and organs vary substantially in size but differ little in morphology; they appear to be scaled versions of a common template or pattern. Such scaling involves adjusting the intrinsic scale of spatial patterns of gene expression that are set up during development to the size of the system. Identifying the mechanisms that regulate scaling of patterns at the tissue, organ and organism level during development is a longstanding challenge in biology, but recent molecular-level data and mathematical modeling have shed light on scaling mechanisms in several systems, including Drosophila and Xenopus. Here, we investigate the underlying principles needed for understanding the mechanisms that can produce scale invariance in spatial pattern formation and discuss examples of systems that scale during development.
Keywords: Bone morphogenetic proteins; Mathematical modeling; Morphogen; Pattern formation; Scale invariance; Turing.
Figures


Similar articles
-
Scaling of morphogen gradients.Curr Opin Genet Dev. 2011 Dec;21(6):704-10. doi: 10.1016/j.gde.2011.07.011. Epub 2011 Aug 26. Curr Opin Genet Dev. 2011. PMID: 21873045 Review.
-
'Big frog, small frog'--maintaining proportions in embryonic development: delivered on 2 July 2008 at the 33rd FEBS Congress in Athens, Greece.FEBS J. 2009 Mar;276(5):1196-207. doi: 10.1111/j.1742-4658.2008.06854.x. FEBS J. 2009. PMID: 19175672
-
Scaling of morphogenetic patterns in reaction-diffusion systems.J Theor Biol. 2016 Sep 7;404:109-119. doi: 10.1016/j.jtbi.2016.05.035. Epub 2016 May 31. J Theor Biol. 2016. PMID: 27255960 Free PMC article.
-
The Decapentaplegic morphogen gradient: from pattern formation to growth regulation.Nat Rev Genet. 2007 Sep;8(9):663-74. doi: 10.1038/nrg2166. Nat Rev Genet. 2007. PMID: 17703237 Review.
-
Modeling digits. Digit patterning is controlled by a Bmp-Sox9-Wnt Turing network modulated by morphogen gradients.Science. 2014 Aug 1;345(6196):566-70. doi: 10.1126/science.1252960. Science. 2014. PMID: 25082703
Cited by
-
Scaling of internal organs during Drosophila embryonic development.Biophys J. 2021 Oct 5;120(19):4264-4276. doi: 10.1016/j.bpj.2021.05.023. Epub 2021 Jun 2. Biophys J. 2021. PMID: 34087212 Free PMC article.
-
Information integration during bioelectric regulation of morphogenesis of the embryonic frog brain.iScience. 2023 Nov 4;26(12):108398. doi: 10.1016/j.isci.2023.108398. eCollection 2023 Dec 15. iScience. 2023. PMID: 38034358 Free PMC article.
-
Spatial pattern formation in microtubule post-translational modifications and the tight localization of motor-driven cargo.J Math Biol. 2017 Apr;74(5):1059-1080. doi: 10.1007/s00285-016-1053-x. Epub 2016 Sep 3. J Math Biol. 2017. PMID: 27592217 Free PMC article.
-
The role of mathematical models in understanding pattern formation in developmental biology.Bull Math Biol. 2015 May;77(5):817-45. doi: 10.1007/s11538-014-0019-7. Epub 2014 Oct 4. Bull Math Biol. 2015. PMID: 25280665 Free PMC article.
-
Self-organization of network dynamics into local quantized states.Sci Rep. 2016 Feb 17;6:21360. doi: 10.1038/srep21360. Sci Rep. 2016. PMID: 26883170 Free PMC article.
References
-
- Alon U. (2007). An Introduction to Systems Biology: Design Principles of Biological Circuits, Vol. 10 Boca Raton, FL: CRC Press;
-
- Aristotle (1910). Historia Animalium (Translation by Thompson D’Arcy Wentworth.). Oxford: Clarendon Press;
-
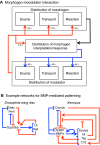
- Ben-Zvi D., Shilo B.-Z., Fainsod A., Barkai N. (2008). Scaling of the BMP morphogen activation gradient in Xenopus embryos. Nature 453, 1205–1211 - PubMed
-
- Ben-Zvi D., Pyrowolakis G., Barkai N., Shilo B. Z. (2011). Expansion-repression mechanism for scaling the Dpp activation gradient in Drosophila wing imaginal discs. Curr. Biol. 21, 1391–1396 - PubMed
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Molecular Biology Databases

