Inversion of a part of the numerator relationship matrix using pedigree information

Abstract

Background: In recent theoretical developments, the information available (e.g. genotypes) divides the original population into two groups: animals with this information (selected animals) and animals without this information (excluded animals). These developments require inversion of the part of the pedigree-based numerator relationship matrix that describes the genetic covariance between selected animals (A22). Our main objective was to propose and evaluate methodology that takes advantage of any potential sparsity in the inverse of A22 in order to reduce the computing time required for its inversion. This potential sparsity is brought out by searching the pedigree for dependencies between the selected animals. Jointly, we expected distant ancestors to provide relationship ties that increase the density of matrix A22 but that their effect on A22-1 might be minor. This hypothesis was also tested.

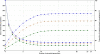
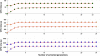
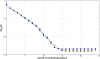
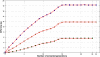
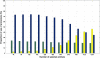
Methods: The inverse of A22 can be computed from the inverse of the triangular factor (T-1) obtained by Cholesky root-free decomposition of A22. We propose an algorithm that sets up the sparsity pattern of T-1 using pedigree information. This algorithm provides positions of the elements of T-1 worth to be computed (i.e. different from zero). A recursive computation of A22-1 is then achieved with or without information on the sparsity pattern and time required for each computation was recorded. For three numbers of selected animals (4000; 8000 and 12 000), A22 was computed using different pedigree extractions and the closeness of the resulting A22-1 to the inverse computed using the fully extracted pedigree was measured by an appropriate norm.

Results: The use of prior information on the sparsity of T-1 decreased the computing time for inversion by a factor of 1.73 on average. Computational issues and practical uses of the different algorithms were discussed. Cases involving more than 12 000 selected animals were considered. Inclusion of 10 generations was determined to be sufficient when computing A22.

Conclusions: Depending on the size and structure of the selected sub-population, gains in time to compute A22-1 are possible and these gains may increase as the number of selected animals increases. Given the sequential nature of most computational steps, the proposed algorithm can benefit from optimization and may be convenient for genomic evaluations.

Figure 1

Small example: a population of 12 animals. Genealogical tree for a population of 12 animals, partitioned in sub-populations 1 (excluded, circle) and 2 (selected, square). Alphabetical order gives the birth order.

Figure 2

Pedigree extraction facts. Generation by generation extraction of the pedigree of the selected population for three size scenarios (green: S4k; orange: S8k; blue: S12k): number of extracted animals (■) and proportion of selected animals in the extracted population (●), expressed as a percentage. Extraction went up to 23 generations for scenario S4k and up to 24 generations for scenarios S8k and S12k.

Figure 3

CPU time required for inversion of A₂₂ by two algorithms. Elapsed CPU time required for inversion of A₂₂ of three different sizes (green: 4000; orange: 8000; blue: 12000), computed using pedigrees with different numbers of extracted generations, by algorithms B (■) and A (●). Red lines show upper and lower confidence intervals (99%; 20 repetitions).

Figure 4

Effect of the depth of the pedigree on${\mathbf{A}}_{\mathbf{22}}^{\mathbf{-}\mathbf{1}}$. Differences, as base-10 logarithm of the norm N, between ${\mathbf{A}}_{\mathbf{22}}^{\mathbf{-}\mathbf{1}}$ based on a pedigree with a limited number of extracted generations and ${\mathbf{A}}_{\mathbf{22}}^{\mathbf{-}\mathbf{1}}$ based on a fully extracted pedigree, for three size scenarios (green: S4k; orange: S8k; blue: S12k).

Figure 5

CPU time required for determination of the sparsity pattern of T^-1. Elapsed CPU time required by the proposed algorithm for determination of the sparsity pattern of T^-1, by number of extracted generations, for three size scenarios (green: S4k, orange: S8k and blue: S12k). Red lines show upper and lower confidence intervals (99%; 20 repetitions).

Figure 6

Degree of sparsity of T^-1. Proportion of null entries in the lower triangular part of T^- 1 for different proportions (%) and numbers (thousands of animals) of selected animals in an extracted population.

Figure 7

Average number of contributors. Average number of contributors by line of T^-1, for different numbers of selected animals (in thousands of animals).

Figure 8

Procedure choice when running algorithm B. Procedure choice (green: EMPTY; yellow: LS; blue: PROD) when running algorithm B, along all line numbers of T^-1, for inversion of matrix A₂₂ with a fully extracted pedigree, for three size scenarios [(a): S4k; (b): S8k ; (c): S12k].

Figure 9

Proportional use of different procedures in algorithm B. Proportional (%) use of the three procedures in algorithm B (green: EMPTY; yellow: LS; blue: PROD), for different numbers of selected animals (in thousands of animals).