Automated fibroglandular tissue segmentation and volumetric density estimation in breast MRI using an atlas-aided fuzzy C-means method

Abstract

Purpose: Breast magnetic resonance imaging (MRI) plays an important role in the clinical management of breast cancer. Studies suggest that the relative amount of fibroglandular (i.e., dense) tissue in the breast as quantified in MR images can be predictive of the risk for developing breast cancer, especially for high-risk women. Automated segmentation of the fibroglandular tissue and volumetric density estimation in breast MRI could therefore be useful for breast cancer risk assessment.

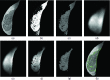
Methods: In this work the authors develop and validate a fully automated segmentation algorithm, namely, an atlas-aided fuzzy C-means (FCM-Atlas) method, to estimate the volumetric amount of fibroglandular tissue in breast MRI. The FCM-Atlas is a 2D segmentation method working on a slice-by-slice basis. FCM clustering is first applied to the intensity space of each 2D MR slice to produce an initial voxelwise likelihood map of fibroglandular tissue. Then a prior learned fibroglandular tissue likelihood atlas is incorporated to refine the initial FCM likelihood map to achieve enhanced segmentation, from which the absolute volume of the fibroglandular tissue (|FGT|) and the relative amount (i.e., percentage) of the |FGT| relative to the whole breast volume (FGT%) are computed. The authors' method is evaluated by a representative dataset of 60 3D bilateral breast MRI scans (120 breasts) that span the full breast density range of the American College of Radiology Breast Imaging Reporting and Data System. The automated segmentation is compared to manual segmentation obtained by two experienced breast imaging radiologists. Segmentation performance is assessed by linear regression, Pearson's correlation coefficients, Student's paired t-test, and Dice's similarity coefficients (DSC).

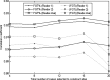
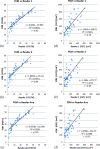
Results: The inter-reader correlation is 0.97 for FGT% and 0.95 for |FGT|. When compared to the average of the two readers' manual segmentation, the proposed FCM-Atlas method achieves a correlation of r = 0.92 for FGT% and r = 0.93 for |FGT|, and the automated segmentation is not statistically significantly different (p = 0.46 for FGT% and p = 0.55 for |FGT|). The bilateral correlation between left breasts and right breasts for the FGT% is 0.94, 0.92, and 0.95 for reader 1, reader 2, and the FCM-Atlas, respectively; likewise, for the |FGT|, it is 0.92, 0.92, and 0.93, respectively. For the spatial segmentation agreement, the automated algorithm achieves a DSC of 0.69 ± 0.1 when compared to reader 1 and 0.61 ± 0.1 for reader 2, respectively, while the DSC between the two readers' manual segmentation is 0.67 ± 0.15. Additional robustness analysis shows that the segmentation performance of the authors' method is stable both with respect to selecting different cases and to varying the number of cases needed to construct the prior probability atlas. The authors' results also show that the proposed FCM-Atlas method outperforms the commonly used two-cluster FCM-alone method. The authors' method runs at ∼5 min for each 3D bilateral MR scan (56 slices) for computing the FGT% and |FGT|, compared to ∼55 min needed for manual segmentation for the same purpose.

Conclusions: The authors' method achieves robust segmentation and can serve as an efficient tool for processing large clinical datasets for quantifying the fibroglandular tissue content in breast MRI. It holds a great potential to support clinical applications in the future including breast cancer risk assessment.

Figure 1

Intrascan fibroglandular likelihood atlas construction. (a) and (b) Two representative slices of a 3D MRI scan with the breast contours plotted. (c) The DTW-based matching of the breast contours between (b) and the generated case-specific 2D breast template. (d) Based on the built point-correspondence in (c), the breast in (b) is deformed to the breast template. (e) The learned case-specific 2D likelihood atlas, where the colorbar indicates voxelwise likelihood of being fibroglandular tissue within the breast template.

Figure 2

Interscan fibroglandular likelihood atlas construction. (a)–(d) Four selected examples of case-specific atlases derived from four different breast MRI cases that have varying fibroglandular tissue amounts, and (e) an overall atlas (i.e., A) learned over the scans of the full training cases (here, 12 cases). The contours delineate the shape of a breast and the contour in (e) represents a generalized standard breast template. The colorbar indicates voxelwise likelihood of fibroglandular tissue.

Figure 3

An example demonstrating the workflow of the proposed FCM-Atlas segmentation method. (a) A representative slice. (b) The adaptive FCM-generated likelihood map (i.e., $u_{ij}^{*}$). (c) The initial segmentation by thresholding $u_{ij}^{*}$. (d) An overall fibroglandular tissue likelihood atlas (i.e., A). (e) The warped likelihood atlas (i.e., W · A) that deforms the standard atlas A to align with the specific slice being processed. (f) The refined likelihood map (i.e., $u_{ij}^{*r}$). (g) The final fibroglandular tissue segmentation by thresholding the refined likelihood map $u_{ij}^{*r}.$ (h) The segmentation contours superimposed on the initial breast MR slice.

Figure 4

Linear regression and correlation between the two readers for the FGT% (r = 0.97) (a) and |FGT| (r = 0.95) (b).

Figure 5

Linear regression between the proposed FCM-Atlas method and the readers’ segmentation for FGT% (left column) and |FGT| (right column). (a) and (d) FCM-Atlas vs reader 1. (b) and (e) FCM-Atlas vs reader 2. (c) and (f) FCM-Atlas vs average of the two readers.

Figure 6

Linear regression and bilateral correlation on the FGT% (left column) and |FGT| measures (right column) between each woman's left and right breasts for reader 1 (a) and (d), reader 2 (b) and (e), and the proposed FCM-Atlas method (c) and (f).

Figure 7

Segmentation performance for our FCM-Atlas method with respect to using a different number of cases to construct the atlas. Note that the horizontal axis is the total case number (i.e., with equal number of cases selected for each BI-RADS density category), and the vertical axis represents the averaged correlation coefficients between the proposed automated FGT segmentation and the manual FGT segmentations (reader 1, reader 2, and their average) of the testing cases.

Figure 8

Segmentation examples for our fully automated FCM-Atlas algorithm with comparison to manual segmentation. Each row shows one case example. (a) Segmented breast. (b) Manual segmentation of reader 1. (c) Manual segmentation of reader 2. (d) The proposed FCM-Atlas based segmentation. (e) Two-cluster FCM-alone based segmentation.

Figure 9

Linear regression and correlation between the automated segmentation of the standard two-cluster FCM-alone method and the readers’ manual segmentation for FGT% (left column) and |FGT| (right column). (a) and (d) Two-cluster FCM-alone vs reader 1. (b) and (e) Two-cluster FCM-alone vs reader 2. (c) and (f) Two-cluster FCM-alone vs average of the two readers.