A theory for how sensorimotor skills are learned and retained in noisy and nonstationary neural circuits
- PMID: 24324147
- PMCID: PMC3876265
- DOI: 10.1073/pnas.1320116110
A theory for how sensorimotor skills are learned and retained in noisy and nonstationary neural circuits
Abstract
During the process of skill learning, synaptic connections in our brains are modified to form motor memories of learned sensorimotor acts. The more plastic the adult brain is, the easier it is to learn new skills or adapt to neurological injury. However, if the brain is too plastic and the pattern of synaptic connectivity is constantly changing, new memories will overwrite old memories, and learning becomes unstable. This trade-off is known as the stability-plasticity dilemma. Here a theory of sensorimotor learning and memory is developed whereby synaptic strengths are perpetually fluctuating without causing instability in motor memory recall, as long as the underlying neural networks are sufficiently noisy and massively redundant. The theory implies two distinct stages of learning--preasymptotic and postasymptotic--because once the error drops to a level comparable to that of the noise-induced error, further error reduction requires altered network dynamics. A key behavioral prediction derived from this analysis is tested in a visuomotor adaptation experiment, and the resultant learning curves are modeled with a nonstationary neural network. Next, the theory is used to model two-photon microscopy data that show, in animals, high rates of dendritic spine turnover, even in the absence of overt behavioral learning. Finally, the theory predicts enhanced task selectivity in the responses of individual motor cortical neurons as the level of task expertise increases. From these considerations, a unique interpretation of sensorimotor memory is proposed--memories are defined not by fixed patterns of synaptic weights but, rather, by nonstationary synaptic patterns that fluctuate coherently.
Keywords: hyperplastic; neural tuning.
Conflict of interest statement
The authors declare no conflict of interest.
Figures

 and
and  . The manifolds are “blurry” because the presence of feedback precludes the need for an exact feed-forward solution. Point P denotes the intersections of these manifolds (and α is the intersection angle). The untrained network exhibits a starting configuration, S, and through the practice/performance of the different skills, the network approaches P. Three learning steps are illustrated. (C) A schematic phase portrait of network behavior as a function of learning rate and noise level. Our network exhibits a high level of irreducible noise (blue “x”), which forces the network into a high learning rate. (D) An example of ill-conditioned oscillatory behavior. Gray lines denote level curves of the error function, and the black lines denote the trajectory in weight space.
. The manifolds are “blurry” because the presence of feedback precludes the need for an exact feed-forward solution. Point P denotes the intersections of these manifolds (and α is the intersection angle). The untrained network exhibits a starting configuration, S, and through the practice/performance of the different skills, the network approaches P. Three learning steps are illustrated. (C) A schematic phase portrait of network behavior as a function of learning rate and noise level. Our network exhibits a high level of irreducible noise (blue “x”), which forces the network into a high learning rate. (D) An example of ill-conditioned oscillatory behavior. Gray lines denote level curves of the error function, and the black lines denote the trajectory in weight space.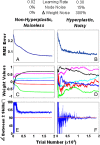
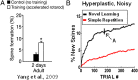
 in the hyperplastic network.
in the hyperplastic network.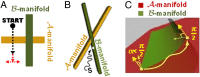
 during the late stage of learning of both skill
during the late stage of learning of both skill  and skill
and skill  when the network is near an orthogonal intersection. The black circle represents the network configuration at the start of the trial, and the dotted lines denote movement from performing skill
when the network is near an orthogonal intersection. The black circle represents the network configuration at the start of the trial, and the dotted lines denote movement from performing skill  . The black dotted line represents the deterministic movement component resulting from error reduction in the direction of the gradient, i.e., perpendicular to the
. The black dotted line represents the deterministic movement component resulting from error reduction in the direction of the gradient, i.e., perpendicular to the  manifold. The red dotted lines represent potential displacements due to noise in the weight change process itself: displacements that can occur both in the direction of the gradient and perpendicular to the gradient. Because of orthogonality, the configuration does not, on average, move away from the
manifold. The red dotted lines represent potential displacements due to noise in the weight change process itself: displacements that can occur both in the direction of the gradient and perpendicular to the gradient. Because of orthogonality, the configuration does not, on average, move away from the  manifold (minimal interference). (B) In early learning, the network configuration approaches an intersection point of the manifolds of desired skills. (C) In late learning, the network explores the space of intersections, tending toward solutions that fulfill the orthogonality constraint.
manifold (minimal interference). (B) In early learning, the network configuration approaches an intersection point of the manifolds of desired skills. (C) In late learning, the network explores the space of intersections, tending toward solutions that fulfill the orthogonality constraint.

References
-
- Hebb DO. The Organization of Behavior. New York: Wiley; 1949.
-
- Hubel DH, Wiesel TN, LeVay S. Plasticity of ocular dominance columns in monkey striate cortex. Philos Trans R Soc Lond B Biol Sci. 1977;278(961):377–409. - PubMed
-
- Carpenter GA, Grossberg S. A massively parallel architecture for a self-organizing neural pattern recognition machine. Comput Vis Graph Image Process. 1987;37(1):54–115.
-
- Haykin S. Neural Networks: A Comprehensive Foundation. Upper Saddle River, NJ: Prentice Hall; 1999.
-
- Jordan MI, Rumelhart DE. Forward models: Supervised learning with a distal teacher. Cogn Sci. 1992;16:307–354.
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources
Medical

