Neurosystems: brain rhythms and cognitive processing
- PMID: 24329933
- PMCID: PMC4916881
- DOI: 10.1111/ejn.12453
Neurosystems: brain rhythms and cognitive processing
Abstract
Neuronal rhythms are ubiquitous features of brain dynamics, and are highly correlated with cognitive processing. However, the relationship between the physiological mechanisms producing these rhythms and the functions associated with the rhythms remains mysterious. This article investigates the contributions of rhythms to basic cognitive computations (such as filtering signals by coherence and/or frequency) and to major cognitive functions (such as attention and multi-modal coordination). We offer support to the premise that the physiology underlying brain rhythms plays an essential role in how these rhythms facilitate some cognitive operations.
Keywords: attention; beta rhythm; coherence filtering; frequency filtering; gamma rhythm.
© 2013 The Authors. European Journal of Neuroscience published by Federation of European Neuroscience Societies and John Wiley & Sons Ltd.
Figures



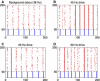
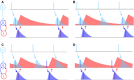


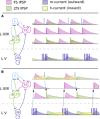
References
-
- Agarwal, R. & Sarma, S.V. (2012) The effects of DBS patterns on basal ganglia activity and thalamic relay. J. Comput. Neurosci., 33, 151–167. - PubMed
-
- Ainsworth, M. , Lee, S. , Cunningham, M.O. , Traub, R.D. , Kopell, N.J. & Whittington, M.A. (2012) Rates and rhythms: a synergistic view of frequency and temporal coding in neuronal networks. Neuron, 75, 572–583. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

