A bioimage informatics based reconstruction of breast tumor microvasculature with computational blood flow predictions
- PMID: 24342178
- PMCID: PMC3977934
- DOI: 10.1016/j.mvr.2013.12.003
A bioimage informatics based reconstruction of breast tumor microvasculature with computational blood flow predictions
Abstract
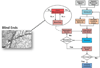
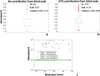
Induction of tumor angiogenesis is among the hallmarks of cancer and a driver of metastatic cascade initiation. Recent advances in high-resolution imaging enable highly detailed three-dimensional geometrical representation of the whole-tumor microvascular architecture. This enormous increase in complexity of image-based data necessitates the application of informatics methods for the analysis, mining and reconstruction of these spatial graph data structures. We present a novel methodology that combines ex-vivo high-resolution micro-computed tomography imaging data with a bioimage informatics algorithm to track and reconstruct the whole-tumor vasculature of a human breast cancer model. The reconstructed tumor vascular network is used as an input of a computational model that estimates blood flow in each segment of the tumor microvascular network. This formulation involves a well-established biophysical model and an optimization algorithm that ensures mass balance and detailed monitoring of all the vessels that feed and drain blood from the tumor microvascular network. Perfusion maps for the whole-tumor microvascular network are computed. Morphological and hemodynamic indices from different regions are compared to infer their role in overall tumor perfusion.
Keywords: Adjacency matrix; BFS; D; DFS; G; IQR; L; L(D); MPL; MTT; Minimum heap; N; P; Priority queue; Q; R; a symmetric matrix consisting of ones and zeros indicating whether or not 2 nodes are connected with a segment; breadth-first search traversal algorithm (systematic visiting of nodes and segments of the graph); data structure where each element is served based on a predefined priority; depth-first search traversal algorithm (systematic visiting of nodes and segments of the graph); flow rate; flow-weighted mean path length; hydraulic conductance; interquartile range (measure of data dispersion); m(tissue); mass of tumor tissue; maximum extravascular diffusion distance of oxygen; pressure; segment diameter; segment length; total mean transit time; total number of segments; tree-based data structure where the parent nodes have always an identity (key) smaller than their children nodes; vascular length density.
Copyright © 2013 Elsevier Inc. All rights reserved.
Figures






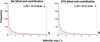



Similar articles
-
Multiscale and multi-modality visualization of angiogenesis in a human breast cancer model.Angiogenesis. 2014 Jul;17(3):695-709. doi: 10.1007/s10456-014-9429-2. Epub 2014 Apr 10. Angiogenesis. 2014. PMID: 24719185 Free PMC article.
-
Vascular phenotyping of the invasive front in breast cancer using a 3D angiogenesis atlas.Microvasc Res. 2023 Sep;149:104555. doi: 10.1016/j.mvr.2023.104555. Epub 2023 May 29. Microvasc Res. 2023. PMID: 37257688 Free PMC article.
-
Dynamic contrast-enhanced micro-computed tomography correlates with 3-dimensional fluorescence ultramicroscopy in antiangiogenic therapy of breast cancer xenografts.Invest Radiol. 2014 Jul;49(7):445-56. doi: 10.1097/RLI.0000000000000038. Invest Radiol. 2014. PMID: 24598441
-
Three-dimensional reconstruction of neovasculature in solid tumors and basement membrane matrix using ex vivo X-ray microcomputed tomography.Microcirculation. 2014 Feb;21(2):159-70. doi: 10.1111/micc.12102. Microcirculation. 2014. PMID: 25279426 Free PMC article.
-
Exploring Graph Traversal Algorithms in Graph-Based Molecular Generation.J Chem Inf Model. 2022 May 9;62(9):2093-2100. doi: 10.1021/acs.jcim.1c00777. Epub 2021 Nov 10. J Chem Inf Model. 2022. PMID: 34757744 Review.
Cited by
-
Computational systems biology approaches to anti-angiogenic cancer therapeutics.Drug Discov Today. 2015 Feb;20(2):187-97. doi: 10.1016/j.drudis.2014.09.026. Epub 2014 Oct 5. Drug Discov Today. 2015. PMID: 25286370 Free PMC article. Review.
-
Quantifying Intratumoral Heterogeneity and Immunoarchitecture Generated In-Silico by a Spatial Quantitative Systems Pharmacology Model.Cancers (Basel). 2023 May 13;15(10):2750. doi: 10.3390/cancers15102750. Cancers (Basel). 2023. PMID: 37345087 Free PMC article.
-
Dynamic Changes in Microvascular Flow Conductivity and Perfusion After Myocardial Infarction Shown by Image-Based Modeling.J Am Heart Assoc. 2019 Apr 2;8(7):e011058. doi: 10.1161/JAHA.118.011058. J Am Heart Assoc. 2019. PMID: 30897998 Free PMC article.
-
Systems biology of angiogenesis signaling: Computational models and omics.WIREs Mech Dis. 2022 Jul;14(4):e1550. doi: 10.1002/wsbm.1550. Epub 2021 Dec 30. WIREs Mech Dis. 2022. PMID: 34970866 Free PMC article. Review.
-
Modelling the transport of fluid through heterogeneous, whole tumours in silico.PLoS Comput Biol. 2019 Jun 21;15(6):e1006751. doi: 10.1371/journal.pcbi.1006751. eCollection 2019 Jun. PLoS Comput Biol. 2019. PMID: 31226169 Free PMC article.
References
-
- Acker JC, et al. Blood perfusion measurements in human tumours: evaluation of laser Doppler methods. Int J Hyperthermia. 1990;6:287–304. - PubMed
-
- Beaney RP, et al. Positron emission tomography for in-vivo measurement of regional blood flow, oxygen utilisation, and blood volume in patients with breast carcinoma. Lancet. 1984;1:131–134. - PubMed
-
- Benedict KF, et al. Hemodynamic systems analysis of capillary network remodeling during the progression of type 2 diabetes. Microcirculation. 2011;18:63–73. - PubMed
-
- Bentley MD, et al. The use of microcomputed tomography to study microvasculature in small rodents. Am J Physiol Regul Integr Comp Physiol. 2002;282:R1267–R1279. - PubMed
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Medical

