Calculation of multi-fractal dimensions in spin chains
- PMID: 24344342
- PMCID: PMC3866471
- DOI: 10.1098/rsta.2012.0520
Calculation of multi-fractal dimensions in spin chains
Abstract
It was demonstrated in Atas & Bogomolny (2012 Phys. Rev. E 86, 021104) that the ground-state wave functions for a large variety of one-dimensional spin- models are multi-fractals in the natural spin-z basis. We present here the details of analytical derivations and numerical confirmations of this statement.
Keywords: ground-state wave function; multi-fractality; spin chains.
Figures
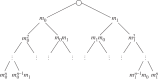
 and
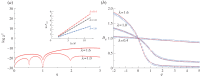
and  . (b) Fractal dimensions for the same measure. Horizontal dashed lines indicate the limiting values
. (b) Fractal dimensions for the same measure. Horizontal dashed lines indicate the limiting values  (2.10). (c) Singularity spectrum for the same measure.
(2.10). (c) Singularity spectrum for the same measure.
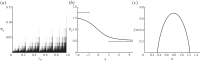
 as a function of
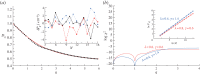
as a function of  for λ=0.4,1,1.6 (top to bottom, respectively). (b) Numerical comparison of the fractal dimensions for the critical QIM obtained by the Lanczos technique with N=3 to 18 (red lines) and exact diagonalization with N=3 to 11 (blue squares). (Online version in colour.)
for λ=0.4,1,1.6 (top to bottom, respectively). (b) Numerical comparison of the fractal dimensions for the critical QIM obtained by the Lanczos technique with N=3 to 18 (red lines) and exact diagonalization with N=3 to 11 (blue squares). (Online version in colour.)
 as a function of
as a function of  for these values of parameters. (Online version in colour.)
for these values of parameters. (Online version in colour.)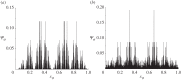
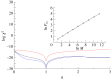
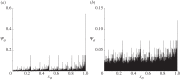
 as a function of
as a function of  where
where  with odd N=3 to 19. (Online version in colour.)
with odd N=3 to 19. (Online version in colour.)References
-
- Heisenberg W. 1928. Zur Theorie des Ferromagnetismus. Z. Phys. 49, 619–636. (10.1007/BF01328601) - DOI
-
- Bethe H. 1931. Zur Theorie der Metalle. Z. Phys. 71, 205–226. (10.1007/BF01341708) - DOI
-
- Baxte RJ. 1982. Exactly solved models in statistical mechanics. New York, NY: Academic Press
-
- Lieb E, Schultz T, Mattis D. 1961. Two soluble models of an antiferromagnetic chain. Ann. Phys. 16, 407–466. (10.1016/0003-4916(61)90115-4) - DOI
-
- Mattis DC. 1994. The many body problem. Singapore: World Scientific
LinkOut - more resources
Full Text Sources
Other Literature Sources
