Spatial dilemmas of diffusible public goods

Abstract

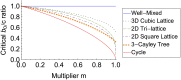
The emergence of cooperation is a central question in evolutionary biology. Microorganisms often cooperate by producing a chemical resource (a public good) that benefits other cells. The sharing of public goods depends on their diffusion through space. Previous theory suggests that spatial structure can promote evolution of cooperation, but the diffusion of public goods introduces new phenomena that must be modeled explicitly. We develop an approach where colony geometry and public good diffusion are described by graphs. We find that the success of cooperation depends on a simple relation between the benefits and costs of the public good, the amount retained by a producer, and the average amount retained by each of the producer's neighbors. These quantities are derived as analytic functions of the graph topology and diffusion rate. In general, cooperation is favored for small diffusion rates, low colony dimensionality, and small rates of decay of the public good. DOI: http://dx.doi.org/10.7554/eLife.01169.001.

Keywords: cooperation; evolutionary graph theory; microbial evolution; social multiplier.

Figure 1.. Colony geometry and public goods sharing in microbes of different shapes.

(A) A two-dimensional colony of S. cerevisiae self-organizes into approximate hexagonal geometry due to the spherical shape of yeast cells. (B) A two-dimensional colony of E. coli, expressing green fluorescent protein, exhibits transient regular-graph-like structure. Panels C and D show idealized graph representations of colony spatial structure, and the consequent sharing of public goods, for sphere-shaped and rod-shaped organisms, respectively. Background colors show the stationary distributions ψ_i of public goods resulting from a single cooperator (center). In each case, the diffusion parameter is set as λ = 3. (C) Two-dimensional colonies of spherical organisms can be represented by triangular lattices with uniform edge weights. (D) Two-dimensional colonies of rod-shaped organisms can be represented using a triangular lattice with unequal weights. In this case, the weights are chosen as 0.1, 0.15 and 0.25, roughly proportional to the shared surface area between E. coli cells when arranged as shown. DOI: http://dx.doi.org/10.7554/eLife.01169.003

Figure 2.. The success of cooperation depends on the amounts of public good retained by a cooperator and its neighbors.

Of the public good that a cooperator produces, a fraction ϕ₀ is retained by the producer, a fraction ϕ₁ is absorbed by each of the cooperator’s nearest neighbors, and the remainder diffuses to cells further away. (For graphs with unequal edge weights, ϕ₁ is the edge-weighted average fraction received by each neighbor.) Cooperation is favored if b/c > 1/(ϕ₀ + ϕ₁), that is, if the benefit bϕ₀ received by producer, plus the average benefit bϕ₁ received by each neighbor, exceeds the cost c of production. This figure shows a triangular lattice with equal edge weights and diffusion parameter λ = 3. DOI: http://dx.doi.org/10.7554/eLife.01169.004

Figure 3.. Cooperation becomes harder to achieve with increasing λ, graph degree and dimensionality, and public goods decay rate.

(A) The critical b/c ratio for public goods production to be favored for various graph structures, plotted against the diffusion rate λ. These results are derived from Equation 2 and the expressions for ϕ₀ in Table 1. For a well-mixed population (complete graph), cooperation is favored if and only if b/c > 1 + λ; for other graph structures, the critical b/c ratio is a increasing, convex function of λ. In general, the conditions for cooperation become increasingly stringent with both the degree and the dimensionality of the graph. (B) Our results are confirmed by simulations on a 15 × 15 periodic triangular lattice with uniform edge weights and cost c = 5%. The critical b/c threshold from Equation 2 is plotted in black. A plus (+) indicates that the frequency of cooperator fixation exceeded the frequency of defector fixation (ρ_C > ρ_D), while a minus (−) indicates the opposite. In all cases the results were statistically significant (two-proportion pooled z-test, p<0.05). (C) Adding decay of rate d effectively reduces both λ and b by the factor 1/(1 + d), reflecting greater locality in sharing but reduced overall concentration of public good. On a graph of b/c versus λ, this moves each point (b/c, λ) along a straight line toward the origin. Since the increase in the critical b/c ratio with λ is in all cases sublinear, this change always hinders cooperation. The critical b/c ratio for a planar triangular lattice is plotted in black. Adding a decay rate equal to the utilization rate (d = 1) changes favorable (b/c, λ) combinations (marked by circles) to unfavorable ones (arrowheads). DOI: http://dx.doi.org/10.7554/eLife.01169.006

Figure 4.. The spread of behaviors on social networks increases with their social multipliers.

In an alternate interpretation of our model, an action has benefits that radiate outward from the actor according to some multiplier m. Individual receiving a large amount of benefit are more likely to be imitated by social contacts. The likelihood of the action to spread—and the benefits to the network as a whole—both increase with the multiplier m. DOI: http://dx.doi.org/10.7554/eLife.01169.007