Is DNA a Good Model Polymer?
- PMID: 24347685
- PMCID: PMC3859536
- DOI: 10.1021/ma401507f
Is DNA a Good Model Polymer?
Abstract
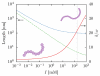
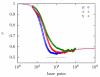
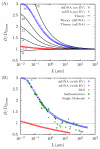
The details surrounding the cross-over from wormlike-specific to universal polymeric behavior has been the subject of debate and confusion even for the simple case of a dilute, unconfined wormlike chain. We have directly computed the polymer size, form factor, free energy and Kirkwood diffusivity for unconfined wormlike chains as a function of molecular weight, focusing on persistence lengths and effective widths that represent single-stranded and double-stranded DNA in a high ionic strength buffer. To do so, we use a chain-growth Monte Carlo algorithm, the Pruned-Enriched Rosenbluth Method (PERM), which allows us to estimate equilibrium and near-equilibrium dynamic properties of wormlike chains over an extremely large range of contour lengths. From our calculations, we find that very large DNA chains (≈ 1,000,000 base pairs depending on the choice of size metric) are required to reach flexible, swollen non-draining coils. Furthermore, our results indicate that the commonly used model polymer λ-DNA (48,500 base pairs) does not exhibit "ideal" scaling, but exists in the middle of the transition to long-chain behavior. We subsequently conclude that typical DNA used in experiments are too short to serve as an accurate model of long-chain, universal polymer behavior.
Figures




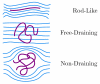
Similar articles
-
Stretching semiflexible polymer chains: evidence for the importance of excluded volume effects from Monte Carlo simulation.J Chem Phys. 2012 Jan 14;136(2):024901. doi: 10.1063/1.3674303. J Chem Phys. 2012. PMID: 22260610
-
Interplay between chain stiffness and excluded volume of semiflexible polymers confined in nanochannels.J Chem Phys. 2014 Feb 28;140(8):084905. doi: 10.1063/1.4865965. J Chem Phys. 2014. PMID: 24588196 Free PMC article.
-
The Backfolded Odijk Regime for Wormlike Chains Confined in Rectangular Nanochannels.Polymers (Basel). 2016 Mar 14;8(3):79. doi: 10.3390/polym8030079. Polymers (Basel). 2016. PMID: 30979173 Free PMC article.
-
Monte Carlo simulations of lattice models for single polymer systems.J Chem Phys. 2014 Oct 28;141(16):164903. doi: 10.1063/1.4899258. J Chem Phys. 2014. PMID: 25362337
-
Simulation of different three-dimensional polymer models of interphase chromosomes compared to experiments-an evaluation and review framework of the 3D genome organization.Semin Cell Dev Biol. 2019 Jun;90:19-42. doi: 10.1016/j.semcdb.2018.07.012. Epub 2018 Aug 24. Semin Cell Dev Biol. 2019. PMID: 30125668 Review.
Cited by
-
Odijk excluded volume interactions during the unfolding of DNA confined in a nanochannel.Macromolecules. 2018 Feb 13;51(3):1172-1180. doi: 10.1021/acs.macromol.7b02466. Epub 2018 Jan 24. Macromolecules. 2018. PMID: 29479117 Free PMC article.
-
Hydrodynamics of DNA confined in nanoslits and nanochannels.Eur Phys J Spec Top. 2014 Dec 1;223(14):3179-3200. doi: 10.1140/epjst/e2014-02326-4. Eur Phys J Spec Top. 2014. PMID: 25566349 Free PMC article.
-
Flow of DNA in micro/nanofluidics: From fundamentals to applications.Biomicrofluidics. 2016 Jul 20;10(4):043403. doi: 10.1063/1.4958719. eCollection 2016 Jul. Biomicrofluidics. 2016. PMID: 27493701 Free PMC article. Review.
-
Single-Polymer Friction Force Microscopy of dsDNA Interacting with a Nanoporous Membrane.Langmuir. 2024 Jan 9;40(1):968-974. doi: 10.1021/acs.langmuir.3c03190. Epub 2023 Dec 20. Langmuir. 2024. PMID: 38117751 Free PMC article.
-
Comparison of microfabricated hexagonal and lamellar post arrays for DNA electrophoresis.Electrophoresis. 2014 Mar;35(5):654-61. doi: 10.1002/elps.201300381. Epub 2013 Nov 27. Electrophoresis. 2014. PMID: 24132597 Free PMC article.
References
-
- de Gennes P-G. Scaling Concepts in Polymer Physics. Cornell University Press; 1979.
-
- Freed KF. Renormalization Group Theory of Macromolecules. John Wiley & Sons, Inc.; 1987.
-
- Rubinstein M, Colby R. Polymer Physics. Oxford University Press: 2003.
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
