Large Covariance Estimation by Thresholding Principal Orthogonal Complements
- PMID: 24348088
- PMCID: PMC3859166
- DOI: 10.1111/rssb.12016
Large Covariance Estimation by Thresholding Principal Orthogonal Complements
Abstract
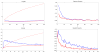
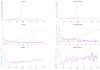
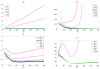
This paper deals with the estimation of a high-dimensional covariance with a conditional sparsity structure and fast-diverging eigenvalues. By assuming sparse error covariance matrix in an approximate factor model, we allow for the presence of some cross-sectional correlation even after taking out common but unobservable factors. We introduce the Principal Orthogonal complEment Thresholding (POET) method to explore such an approximate factor structure with sparsity. The POET estimator includes the sample covariance matrix, the factor-based covariance matrix (Fan, Fan, and Lv, 2008), the thresholding estimator (Bickel and Levina, 2008) and the adaptive thresholding estimator (Cai and Liu, 2011) as specific examples. We provide mathematical insights when the factor analysis is approximately the same as the principal component analysis for high-dimensional data. The rates of convergence of the sparse residual covariance matrix and the conditional sparse covariance matrix are studied under various norms. It is shown that the impact of estimating the unknown factors vanishes as the dimensionality increases. The uniform rates of convergence for the unobserved factors and their factor loadings are derived. The asymptotic results are also verified by extensive simulation studies. Finally, a real data application on portfolio allocation is presented.
Keywords: High-dimensionality; approximate factor model; cross-sectional correlation; diverging eigenvalues; low-rank matrix; principal components; sparse matrix; thresholding; unknown factors.
Figures

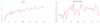



Similar articles
-
Asymptotics of empirical eigenstructure for high dimensional spiked covariance.Ann Stat. 2017 Jun;45(3):1342-1374. doi: 10.1214/16-AOS1487. Epub 2017 Jun 13. Ann Stat. 2017. PMID: 28835726 Free PMC article.
-
HIGH DIMENSIONAL COVARIANCE MATRIX ESTIMATION IN APPROXIMATE FACTOR MODELS.Ann Stat. 2011 Jan 1;39(6):3320-3356. doi: 10.1214/11-AOS944. Ann Stat. 2011. PMID: 22661790 Free PMC article.
-
LARGE COVARIANCE ESTIMATION THROUGH ELLIPTICAL FACTOR MODELS.Ann Stat. 2018 Aug;46(4):1383-1414. doi: 10.1214/17-AOS1588. Epub 2018 Jun 27. Ann Stat. 2018. PMID: 30214095 Free PMC article.
-
Threshold selection for covariance estimation.Biometrics. 2019 Sep;75(3):895-905. doi: 10.1111/biom.13048. Epub 2019 Apr 3. Biometrics. 2019. PMID: 30820943
-
Robust High-dimensional Volatility Matrix Estimation for High-Frequency Factor Model.J Am Stat Assoc. 2018;113(523):1268-1283. doi: 10.1080/01621459.2017.1340888. Epub 2018 Oct 8. J Am Stat Assoc. 2018. PMID: 30906083 Free PMC article.
Cited by
-
TGCnA: temporal gene coexpression network analysis using a low-rank plus sparse framework.J Appl Stat. 2019 Sep 16;47(6):1064-1083. doi: 10.1080/02664763.2019.1667311. eCollection 2020. J Appl Stat. 2019. PMID: 35706920 Free PMC article.
-
A SHRINKAGE PRINCIPLE FOR HEAVY-TAILED DATA: HIGH-DIMENSIONAL ROBUST LOW-RANK MATRIX RECOVERY.Ann Stat. 2021 Jun;49(3):1239-1266. doi: 10.1214/20-aos1980. Epub 2021 Aug 9. Ann Stat. 2021. PMID: 34556893 Free PMC article.
-
Inference and uncertainty quantification for noisy matrix completion.Proc Natl Acad Sci U S A. 2019 Nov 12;116(46):22931-22937. doi: 10.1073/pnas.1910053116. Epub 2019 Oct 30. Proc Natl Acad Sci U S A. 2019. PMID: 31666329 Free PMC article.
-
Sparsifying the Fisher Linear Discriminant by Rotation.J R Stat Soc Series B Stat Methodol. 2015 Sep 1;77(4):827-851. doi: 10.1111/rssb.12092. Epub 2014 Nov 7. J R Stat Soc Series B Stat Methodol. 2015. PMID: 26512210 Free PMC article.
-
Extracting Conditionally Heteroskedastic Components using Independent Component Analysis.J Time Ser Anal. 2020 Mar;41(2):293-311. doi: 10.1111/jtsa.12505. Epub 2019 Sep 8. J Time Ser Anal. 2020. PMID: 32508370 Free PMC article.
References
-
- Agarwal A, Negahban S, Martin J, Wainwright MJ. Noisy matrix decomposition via convex relaxation: Optimal rates in high dimensions. Ann Statist. 2012;40:1171–1197.
-
- Ahn S, Lee Y, Schmidt P. GMM estimation of linear panel data models with time-varying individual effects. J Econometrics. 2001;101:219–255.
-
- Alessi L, Barigozzi M, Capassoc M. Improved penalization for determining the number of factors in approximate factor models. Statistics and Probability Letters. 2010;80:1806–1813.
-
- Amini AA, Wainwright MJ. High-dimensional analysis of semidefinite relaxations for sparse principal components. Ann Statist. 2009;37:2877–2921.
-
- Antoniadis A, Fan J. Regularized wavelet approximations. J Amer Statist Assoc. 2001;96:939–967.
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
