Modeling the afferent dynamics of the baroreflex control system
- PMID: 24348231
- PMCID: PMC3861044
- DOI: 10.1371/journal.pcbi.1003384
Modeling the afferent dynamics of the baroreflex control system
Abstract
In this study we develop a modeling framework for predicting baroreceptor firing rate as a function of blood pressure. We test models within this framework both quantitatively and qualitatively using data from rats. The models describe three components: arterial wall deformation, stimulation of mechanoreceptors located in the BR nerve-endings, and modulation of the action potential frequency. The three sub-systems are modeled individually following well-established biological principles. The first submodel, predicting arterial wall deformation, uses blood pressure as an input and outputs circumferential strain. The mechanoreceptor stimulation model, uses circumferential strain as an input, predicting receptor deformation as an output. Finally, the neural model takes receptor deformation as an input predicting the BR firing rate as an output. Our results show that nonlinear dependence of firing rate on pressure can be accounted for by taking into account the nonlinear elastic properties of the artery wall. This was observed when testing the models using multiple experiments with a single set of parameters. We find that to model the response to a square pressure stimulus, giving rise to post-excitatory depression, it is necessary to include an integrate-and-fire model, which allows the firing rate to cease when the stimulus falls below a given threshold. We show that our modeling framework in combination with sensitivity analysis and parameter estimation can be used to test and compare models. Finally, we demonstrate that our preferred model can exhibit all known dynamics and that it is advantageous to combine qualitative and quantitative analysis methods.
Conflict of interest statement
The authors have declared that no competing interests exist.
Figures



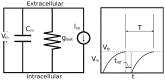
 Voigt bodies (a parallel spring and dashpot) in series shown here describes the strain sensed by the mechanoreceptors relative to the deformation of the arterial wall. The spring
Voigt bodies (a parallel spring and dashpot) in series shown here describes the strain sensed by the mechanoreceptors relative to the deformation of the arterial wall. The spring  represents the elasticity of the BR nerve endings, whereas the
represents the elasticity of the BR nerve endings, whereas the  Voigt bodies reflect the viscoelastic properties of the surrounding connective tissue. Each element
Voigt bodies reflect the viscoelastic properties of the surrounding connective tissue. Each element  provides a timescale adaptation of BRs firing rate in response to a step increase in pressure observed in experiments. This study compares the cases
provides a timescale adaptation of BRs firing rate in response to a step increase in pressure observed in experiments. This study compares the cases  .
.
 ,
,  and
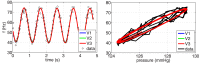
and  (denoted in the legend as V1, V2, and V3, respectively), listed in Table 3. The optimized parameter values, the
(denoted in the legend as V1, V2, and V3, respectively), listed in Table 3. The optimized parameter values, the  and the RMSE errors are reported in Table 4.
and the RMSE errors are reported in Table 4.
 ,
,  and
and  (denoted in the legend as V1, V2, and V3, respectively) to reproduce four types of increases in pressure: ((A) 128 mmHg, (B) 134 mmHg, (C) 137 mmHg, and (D) 143 mmHg) published by Brown . The parameters of each model have been optimized for each data set individually and are listed in Table 4 together with the
(denoted in the legend as V1, V2, and V3, respectively) to reproduce four types of increases in pressure: ((A) 128 mmHg, (B) 134 mmHg, (C) 137 mmHg, and (D) 143 mmHg) published by Brown . The parameters of each model have been optimized for each data set individually and are listed in Table 4 together with the  and the RMSE errors.
and the RMSE errors.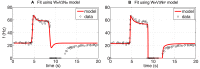
 and the RMSE errors.
and the RMSE errors.
 . Note, that the overshoot is diminished for responses to smaller step-increases in pressure, and that the baseline firing rate is not reproduced accurately. (B) Predictions obtained with the nonlinear model
. Note, that the overshoot is diminished for responses to smaller step-increases in pressure, and that the baseline firing rate is not reproduced accurately. (B) Predictions obtained with the nonlinear model  accounting for nonlinear stiffening with increased pressure allowed us to accurately fit all four responses using one set of parameter values.
accounting for nonlinear stiffening with increased pressure allowed us to accurately fit all four responses using one set of parameter values.
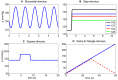
 to various pressure stimuli including sinusoidal (A), ramp up (B), step-increase (C), and trianglular (D) showing the model's ability to reflect rectification (A), saturation (B), two time-scale adaptation (C), and asymmetry (D).
to various pressure stimuli including sinusoidal (A), ramp up (B), step-increase (C), and trianglular (D) showing the model's ability to reflect rectification (A), saturation (B), two time-scale adaptation (C), and asymmetry (D).Similar articles
-
A model-based analysis of autonomic nervous function in response to the Valsalva maneuver.J Appl Physiol (1985). 2019 Nov 1;127(5):1386-1402. doi: 10.1152/japplphysiol.00015.2019. Epub 2019 Aug 1. J Appl Physiol (1985). 2019. PMID: 31369335 Free PMC article.
-
Pharmacological assessment of the contribution of the arterial baroreflex to sympathetic discharge patterns in healthy humans.J Neurophysiol. 2018 Jun 1;119(6):2166-2175. doi: 10.1152/jn.00935.2017. Epub 2018 Feb 28. J Neurophysiol. 2018. PMID: 29488839 Free PMC article.
-
Dynamic characteristics of carotid sinus pressure-nerve activity transduction in rabbits.Jpn J Physiol. 2005 Jun;55(3):157-63. doi: 10.2170/jjphysiol.R2122. Epub 2005 Aug 5. Jpn J Physiol. 2005. PMID: 16079025
-
[Baroreflex sensitivity].Ital Heart J Suppl. 2001 May;2(5):472-7. Ital Heart J Suppl. 2001. PMID: 11388329 Review. Italian.
-
Role of arterial baroreceptor function on cardiovascular adjustments to acute and chronic dynamic exercise.Biol Res. 1998;31(3):273-9. Biol Res. 1998. PMID: 9830515 Review.
Cited by
-
Modeling the differentiation of A- and C-type baroreceptor firing patterns.J Comput Neurosci. 2017 Feb;42(1):11-30. doi: 10.1007/s10827-016-0624-6. Epub 2016 Oct 5. J Comput Neurosci. 2017. PMID: 27704337 Free PMC article.
-
Data Driven Control of Vagus Nerve Stimulation for the Cardiovascular System: An in Silico Computational Study.Front Physiol. 2022 Jun 3;13:798157. doi: 10.3389/fphys.2022.798157. eCollection 2022. Front Physiol. 2022. PMID: 35721533 Free PMC article.
-
Structural correlation method for model reduction and practical estimation of patient specific parameters illustrated on heart rate regulation.Math Biosci. 2014 Nov;257:50-9. doi: 10.1016/j.mbs.2014.07.003. Epub 2014 Jul 19. Math Biosci. 2014. PMID: 25050793 Free PMC article.
-
Blood pressure is maintained during dehydration by hypothalamic paraventricular nucleus-driven tonic sympathetic nerve activity.J Physiol. 2014 Sep 1;592(17):3783-99. doi: 10.1113/jphysiol.2014.276261. Epub 2014 Jun 27. J Physiol. 2014. PMID: 24973410 Free PMC article.
-
A model of anaerobic tissue perfusion during trauma-Lactate trajectory curvature can determine recovery.PLoS Comput Biol. 2025 Aug 11;21(8):e1012820. doi: 10.1371/journal.pcbi.1012820. eCollection 2025 Aug. PLoS Comput Biol. 2025. PMID: 40788942 Free PMC article.
References
-
- Kardos A, Simon Rudas J, Gingl Z, Csanady M (1997) Effect of postural changes on arterial baroreflex sensitivity assessed by the spontaneous sequence method and valsalva manoeuvre in healthy subjects. Clin Autonom Res 7: 143–148. - PubMed
-
- Boron WF, Boulpaep EL (2005) Medical physiology: A cellular and molecular approach. Philadelphia, PA: Elsevier.
-
- Guyton AC, Hall JE (2006) Guyton and Hall Textbook of Medical Physiology. Philadelphia: Elsevier Saunders., 11th edition.
-
- Cowley AWJ (1992) Long-term control of arterial blood pressure. Physiol Rev 72: 231–300. - PubMed
-
- Ketch T, Biaggioni I, Robertson RM, Robertson D (2002) Four faces of baroreflex failure. hypertensive crisis, volatile hypertension, orthostatic tachycardia, and malignant vagotonia. Circulation 105: 2518–2523. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

