Motor learning of novel dynamics is not represented in a single global coordinate system: evaluation of mixed coordinate representations and local learning
- PMID: 24353296
- PMCID: PMC3949315
- DOI: 10.1152/jn.00493.2013
Motor learning of novel dynamics is not represented in a single global coordinate system: evaluation of mixed coordinate representations and local learning
Abstract
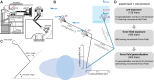
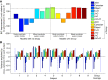
Successful motor performance requires the ability to adapt motor commands to task dynamics. A central question in movement neuroscience is how these dynamics are represented. Although it is widely assumed that dynamics (e.g., force fields) are represented in intrinsic, joint-based coordinates (Shadmehr R, Mussa-Ivaldi FA. J Neurosci 14: 3208-3224, 1994), recent evidence has questioned this proposal. Here we reexamine the representation of dynamics in two experiments. By testing generalization following changes in shoulder, elbow, or wrist configurations, the first experiment tested for extrinsic, intrinsic, or object-centered representations. No single coordinate frame accounted for the pattern of generalization. Rather, generalization patterns were better accounted for by a mixture of representations or by models that assumed local learning and graded, decaying generalization. A second experiment, in which we replicated the design of an influential study that had suggested encoding in intrinsic coordinates (Shadmehr and Mussa-Ivaldi 1994), yielded similar results. That is, we could not find evidence that dynamics are represented in a single coordinate system. Taken together, our experiments suggest that internal models do not employ a single coordinate system when generalizing and may well be represented as a mixture of coordinate systems, as a single system with local learning, or both.
Keywords: coordinate frames; internal models; intralimb generalization; motor adaptation; motor control.
Figures











References
-
- Burgess JK, Bareither R, Patton JL. Single limb performance following contralateral bimanual limb training. IEEE Trans Neural Syst Rehabil Eng 15: 347–355, 2007 - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

