Emerging predictable features of replicated biological invasion fronts
- PMID: 24367086
- PMCID: PMC3890861
- DOI: 10.1073/pnas.1321167110
Emerging predictable features of replicated biological invasion fronts
Abstract
Biological dispersal shapes species' distribution and affects their coexistence. The spread of organisms governs the dynamics of invasive species, the spread of pathogens, and the shifts in species ranges due to climate or environmental change. Despite its relevance for fundamental ecological processes, however, replicated experimentation on biological dispersal is lacking, and current assessments point at inherent limitations to predictability, even in the simplest ecological settings. In contrast, we show, by replicated experimentation on the spread of the ciliate Tetrahymena sp. in linear landscapes, that information on local unconstrained movement and reproduction allows us to predict reliably the existence and speed of traveling waves of invasion at the macroscopic scale. Furthermore, a theoretical approach introducing demographic stochasticity in the Fisher-Kolmogorov framework of reaction-diffusion processes captures the observed fluctuations in range expansions. Therefore, predictability of the key features of biological dispersal overcomes the inherent biological stochasticity. Our results establish a causal link from the short-term individual level to the long-term, broad-scale population patterns and may be generalized, possibly providing a general predictive framework for biological invasions in natural environments.
Keywords: Fisher wave; colonization; frontiers; microcosm; spatial.
Conflict of interest statement
The authors declare no conflict of interest.
Figures
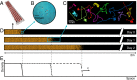
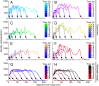
 generations). (G and H) Two dispersal events simulated according to the generalized model equation, with initial conditions as at the second experimental time point. Data are binned in 5-cm intervals, typical length scale of the process.
generations). (G and H) Two dispersal events simulated according to the generalized model equation, with initial conditions as at the second experimental time point. Data are binned in 5-cm intervals, typical length scale of the process.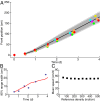
 and
and  confidence intervals computed by numerically integrating the generalized model equation, with initial conditions as at the second experimental time point, in 1,020 iterations. The black curve is the mean front position in the stochastic integrations. (B) The increase in range variability between replicates in the dispersal experiment (blue diamonds) is well described by the stochastic model (red line). (C) Mean front speed for different choices of the reference density value at which we estimated the front position in the experiment; error bars are smaller than symbols.
confidence intervals computed by numerically integrating the generalized model equation, with initial conditions as at the second experimental time point, in 1,020 iterations. The black curve is the mean front position in the stochastic integrations. (B) The increase in range variability between replicates in the dispersal experiment (blue diamonds) is well described by the stochastic model (red line). (C) Mean front speed for different choices of the reference density value at which we estimated the front position in the experiment; error bars are smaller than symbols.Similar articles
-
Highly variable spread rates in replicated biological invasions: fundamental limits to predictability.Science. 2009 Sep 18;325(5947):1536-9. doi: 10.1126/science.1176138. Science. 2009. PMID: 19762641
-
The importance of being atomic: Ecological invasions as random walks instead of waves.Theor Popul Biol. 2016 Dec;112:157-169. doi: 10.1016/j.tpb.2016.06.002. Epub 2016 Jul 11. Theor Popul Biol. 2016. PMID: 27417408
-
Global Distribution of Alien Mammals Under Climate Change.Glob Chang Biol. 2024 Nov;30(11):e17560. doi: 10.1111/gcb.17560. Glob Chang Biol. 2024. PMID: 39545282
-
Environmental Adaptations, Ecological Filtering, and Dispersal Central to Insect Invasions.Annu Rev Entomol. 2018 Jan 7;63:345-368. doi: 10.1146/annurev-ento-020117-043315. Epub 2017 Oct 13. Annu Rev Entomol. 2018. PMID: 29029589 Review.
-
Novel insights on population and range edge dynamics using an unparalleled spatiotemporal record of species invasion.J Anim Ecol. 2018 May;87(3):581-593. doi: 10.1111/1365-2656.12755. Epub 2017 Oct 17. J Anim Ecol. 2018. PMID: 28892141 Review.
Cited by
-
Range expansions transition from pulled to pushed waves as growth becomes more cooperative in an experimental microbial population.Proc Natl Acad Sci U S A. 2016 Jun 21;113(25):6922-7. doi: 10.1073/pnas.1521056113. Epub 2016 May 16. Proc Natl Acad Sci U S A. 2016. PMID: 27185918 Free PMC article.
-
The ecological roles of bacterial chemotaxis.Nat Rev Microbiol. 2022 Aug;20(8):491-504. doi: 10.1038/s41579-022-00709-w. Epub 2022 Mar 15. Nat Rev Microbiol. 2022. PMID: 35292761 Review.
-
Finite-size effects on bacterial population expansion under controlled flow conditions.Sci Rep. 2017 Mar 6;7:43903. doi: 10.1038/srep43903. Sci Rep. 2017. PMID: 28262769 Free PMC article.
-
Infection in patchy populations: Contrasting pathogen invasion success and dispersal at varying times since host colonization.Evol Lett. 2019 Sep 24;3(5):555-566. doi: 10.1002/evl3.141. eCollection 2019 Oct. Evol Lett. 2019. PMID: 31636946 Free PMC article.
-
Disturbance reverses classic biodiversity predictions in river-like landscapes.Proc Biol Sci. 2018 Dec 19;285(1893):20182441. doi: 10.1098/rspb.2018.2441. Proc Biol Sci. 2018. PMID: 30963914 Free PMC article.
References
-
- Fisher RA. The wave of advance of advantageous genes. Ann Eugen. 1937;7:355–369.
-
- Kolmogorov AN, Petrovskii IG, Piskunov NS. A study of the diffusion equation with increase in the amount of substance, and its application to a biological problem. Bull. Moscow Univ. Math. Mech. 1937;1(1):1–25.
-
- Skellam JG. Random dispersal in theoretical populations. Biometrika. 1951;38(1-2):196–218. - PubMed
-
- Elton CS. The Ecology of Invasions by Animals and Plants. London: Methuen; 1958.
-
- Andow DA, Kareiva PM, Levin SA, Okubo A. Spread of invading organisms. Landscape Ecol. 1990;4(2/3):177–188.
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Molecular Biology Databases

