Perturbation biology: inferring signaling networks in cellular systems
- PMID: 24367245
- PMCID: PMC3868523
- DOI: 10.1371/journal.pcbi.1003290
Perturbation biology: inferring signaling networks in cellular systems
Abstract
We present a powerful experimental-computational technology for inferring network models that predict the response of cells to perturbations, and that may be useful in the design of combinatorial therapy against cancer. The experiments are systematic series of perturbations of cancer cell lines by targeted drugs, singly or in combination. The response to perturbation is quantified in terms of relative changes in the measured levels of proteins, phospho-proteins and cellular phenotypes such as viability. Computational network models are derived de novo, i.e., without prior knowledge of signaling pathways, and are based on simple non-linear differential equations. The prohibitively large solution space of all possible network models is explored efficiently using a probabilistic algorithm, Belief Propagation (BP), which is three orders of magnitude faster than standard Monte Carlo methods. Explicit executable models are derived for a set of perturbation experiments in SKMEL-133 melanoma cell lines, which are resistant to the therapeutically important inhibitor of RAF kinase. The resulting network models reproduce and extend known pathway biology. They empower potential discoveries of new molecular interactions and predict efficacious novel drug perturbations, such as the inhibition of PLK1, which is verified experimentally. This technology is suitable for application to larger systems in diverse areas of molecular biology.
Conflict of interest statement
The authors have declared that no competing interests exist.
Figures


 factors except that from the cavity constraint μ. Distributions centered on zero denote unlikely interactions (see j = 2), centered on the right of zero denote likely positive interactions (see j = 3), and centered on the left denote likely negative interactions (see j = N). These distributions inform the parameters of the Gaussian distribution for the mean-field, aggregate sum variable
factors except that from the cavity constraint μ. Distributions centered on zero denote unlikely interactions (see j = 2), centered on the right of zero denote likely positive interactions (see j = 3), and centered on the left denote likely negative interactions (see j = N). These distributions inform the parameters of the Gaussian distribution for the mean-field, aggregate sum variable  . The distribution
. The distribution  summarizes the state of the non-cavity parameters. Bottom panel: we calculate the probability of each possible parameter assignment
summarizes the state of the non-cavity parameters. Bottom panel: we calculate the probability of each possible parameter assignment  to the cavity parameter wik constrained to the data in the cavity condition. This calculation boils down to a simple convolution of the fitness function with a fixed parameter assignment
to the cavity parameter wik constrained to the data in the cavity condition. This calculation boils down to a simple convolution of the fitness function with a fixed parameter assignment  with the probability of the aggregate sum variable
with the probability of the aggregate sum variable  , obtained by integrating over all values of
, obtained by integrating over all values of  . Each assignment
. Each assignment  contributes proportional to the area under the curve. The resulting update is the contribution of condition μ on the distribution of
contributes proportional to the area under the curve. The resulting update is the contribution of condition μ on the distribution of  , denoted
, denoted  . This recently updated distribution becomes part of the global information for successive updates to other parameters.
. This recently updated distribution becomes part of the global information for successive updates to other parameters.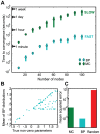



References
-
- Hanahan D, Weinberg RA (2011) Hallmarks of cancer: the next generation. Cell 144: 646–674. - PubMed
-
- Druker BJ, Talpaz M, Resta DJ, Peng B, Buchdunger E, et al. (2001) Efficacy and safety of a specific inhibitor of the BCR-ABL tyrosine kinase in chronic myeloid leukemia. N Engl J Med 344: 1031–1037. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Research Materials
Miscellaneous

