Electrodiffusive model for astrocytic and neuronal ion concentration dynamics
- PMID: 24367247
- PMCID: PMC3868551
- DOI: 10.1371/journal.pcbi.1003386
Electrodiffusive model for astrocytic and neuronal ion concentration dynamics
Abstract
The cable equation is a proper framework for modeling electrical neural signalling that takes place at a timescale at which the ionic concentrations vary little. However, in neural tissue there are also key dynamic processes that occur at longer timescales. For example, endured periods of intense neural signaling may cause the local extracellular K(+)-concentration to increase by several millimolars. The clearance of this excess K(+) depends partly on diffusion in the extracellular space, partly on local uptake by astrocytes, and partly on intracellular transport (spatial buffering) within astrocytes. These processes, that take place at the time scale of seconds, demand a mathematical description able to account for the spatiotemporal variations in ion concentrations as well as the subsequent effects of these variations on the membrane potential. Here, we present a general electrodiffusive formalism for modeling of ion concentration dynamics in a one-dimensional geometry, including both the intra- and extracellular domains. Based on the Nernst-Planck equations, this formalism ensures that the membrane potential and ion concentrations are in consistency, it ensures global particle/charge conservation and it accounts for diffusion and concentration dependent variations in resistivity. We apply the formalism to a model of astrocytes exchanging ions with the extracellular space. The simulations show that K(+)-removal from high-concentration regions is driven by a local depolarization of the astrocyte membrane, which concertedly (i) increases the local astrocytic uptake of K(+), (ii) suppresses extracellular transport of K(+), (iii) increases axial transport of K(+) within astrocytes, and (iv) facilitates astrocytic relase of K(+) in regions where the extracellular concentration is low. Together, these mechanisms seem to provide a robust regulatory scheme for shielding the extracellular space from excess K(+).
Conflict of interest statement
The authors have declared that no competing interests exist.
Figures
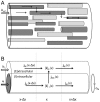
 and an arbitrary extension
and an arbitrary extension  in the
in the  -direction. The tissue contains cells (dark grey) that participate in the transport process, and cells that do not (light grey). (B) The interior of all participatory cells represented as a single, equivalent cylindrical cable (
-direction. The tissue contains cells (dark grey) that participate in the transport process, and cells that do not (light grey). (B) The interior of all participatory cells represented as a single, equivalent cylindrical cable ( ), coated by ECS (
), coated by ECS ( ). The geometry is specified by three parameters, where
). The geometry is specified by three parameters, where  and
and  are, respectively, the fractions of
are, respectively, the fractions of  occupied by the ICS of participatory cells and the ECS, and
occupied by the ICS of participatory cells and the ECS, and  is the amount of membrane area per tissue volume (or, equivalently, the circumference of the equivalent cable divided by
is the amount of membrane area per tissue volume (or, equivalently, the circumference of the equivalent cable divided by  ). Due to the presence of other cells (non-participatory), we generally have that
). Due to the presence of other cells (non-participatory), we generally have that  . The concentration of ion species
. The concentration of ion species  is denoted
is denoted  where
where  represents domain
represents domain  or
or  . Ionic movement is described by the transmembrane flux density (
. Ionic movement is described by the transmembrane flux density ( ) and the longitudinal flux densities due to electrical migration (
) and the longitudinal flux densities due to electrical migration ( ) and diffusion (
) and diffusion ( ).
).
 ) and “−” should be used for the extracellular domain (
) and “−” should be used for the extracellular domain ( ). The formalism is general to the choice of membrane mechanisms.
). The formalism is general to the choice of membrane mechanisms.  , representing system specific membrane mechanisms (ion pumps, ion channels, cotransporters ect.), must to be specified by the user. External input to the system must also be specified. The input must be locally electroneutral, i.e., must fulfill
, representing system specific membrane mechanisms (ion pumps, ion channels, cotransporters ect.), must to be specified by the user. External input to the system must also be specified. The input must be locally electroneutral, i.e., must fulfill  .
.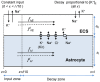
 or diffusion
or diffusion  through the ICS (
through the ICS ( ) or ECS (
) or ECS ( ). The cation-exchange input was a constant influx of K+ and efflux of Na+ to/from the ECS of the input zone (defined as the region
). The cation-exchange input was a constant influx of K+ and efflux of Na+ to/from the ECS of the input zone (defined as the region  ). The cation-exchange output was an efflux of K+ and influx Na+ from/to the ECS. The output was proportional to the local K+-concentration, and occurred over the whole axis. The decay zone was defined as the part of the axis where no input was applied (
). The cation-exchange output was an efflux of K+ and influx Na+ from/to the ECS. The output was proportional to the local K+-concentration, and occurred over the whole axis. The decay zone was defined as the part of the axis where no input was applied ( ), i.e., the region where there was a net efflux of K+ from the system.
), i.e., the region where there was a net efflux of K+ from the system.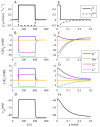
 ) in the input zone. (E–H) Spatial profiles of selected variables at a time
) in the input zone. (E–H) Spatial profiles of selected variables at a time  , when the system was in steady state. The constant cation-exchange input was applied to the ECS of the input (
, when the system was in steady state. The constant cation-exchange input was applied to the ECS of the input ( ) zone from
) zone from  to
to  . (A) The input and output flux densities of K+ to the point
. (A) The input and output flux densities of K+ to the point  . We recall that the Na+ input/output (not shown) was the opposite of that of K+:
. We recall that the Na+ input/output (not shown) was the opposite of that of K+:  and
and  . (B,D) During the input, ion concentrations in the ECS and ICS changed, but reached steady state after about 10–50 s after stimulus onset. (B)
. (B,D) During the input, ion concentrations in the ECS and ICS changed, but reached steady state after about 10–50 s after stimulus onset. (B)  (at
(at  ) had then increased by about 7.7 mM with respect to the baseline value. (C)
) had then increased by about 7.7 mM with respect to the baseline value. (C)  had increased by about 12.5 mM due to uptake by the astrocyte. (D) The astrocytic membrane potential had been depolarized to about −59 mV at
had increased by about 12.5 mM due to uptake by the astrocyte. (D) The astrocytic membrane potential had been depolarized to about −59 mV at  . The impact of the input was smaller outside the input zone. (F–H) Deviations from the baseline ionic concentrations and
. The impact of the input was smaller outside the input zone. (F–H) Deviations from the baseline ionic concentrations and  typically decreased with
typically decreased with  . Far away from the input zone (
. Far away from the input zone ( ), the conditions were close to the baseline conditions. (B–C, F–G) Ionic concentrations were represented in terms of deviations from resting concentrations:
), the conditions were close to the baseline conditions. (B–C, F–G) Ionic concentrations were represented in terms of deviations from resting concentrations:  for
for  . For direct comparison with ion concentrations, the charge density was represented as an equivalent concentration of unit charges
. For direct comparison with ion concentrations, the charge density was represented as an equivalent concentration of unit charges  .
.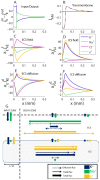
 ). (B) Transmembrane flux densities. (C–F) Longitudinal flux densities due to (C) electrical migration in the ECS, (D) electrical migration in the ICS, (E) diffusion in the ECS and (F) diffusion in the ICS. (A–D) To aid comparison, flux densities
). (B) Transmembrane flux densities. (C–F) Longitudinal flux densities due to (C) electrical migration in the ECS, (D) electrical migration in the ICS, (E) diffusion in the ECS and (F) diffusion in the ICS. (A–D) To aid comparison, flux densities  were scaled by the relative area fraction
were scaled by the relative area fraction  (e.g., if
(e.g., if  ,
,  and
and  carry the same the net flux of ion species
carry the same the net flux of ion species  ). (G) A flow chart that qualitatively summarizes the essential information in (A–F), showing the main transport routes of K+ and Na+ during SS (Cl− excluded from the overview). K+ generally entered the system in the input zone and left the system from some point along the astrocyte axis. The transport route of K+ (from entering to leaving the system) was predominantly intracellular, demonstrating the astrocyte's efficiency as a spatial buffer. Na+ entered in the decay zone and left from the input zone. Na+ transport predominantly took place in the ECS. The illustration (G) is qualitative - longer arrows mean higher flux densities, but the mapping from (A–F) to (G) is not quantitatively exact. The input zone was in the region
). (G) A flow chart that qualitatively summarizes the essential information in (A–F), showing the main transport routes of K+ and Na+ during SS (Cl− excluded from the overview). K+ generally entered the system in the input zone and left the system from some point along the astrocyte axis. The transport route of K+ (from entering to leaving the system) was predominantly intracellular, demonstrating the astrocyte's efficiency as a spatial buffer. Na+ entered in the decay zone and left from the input zone. Na+ transport predominantly took place in the ECS. The illustration (G) is qualitative - longer arrows mean higher flux densities, but the mapping from (A–F) to (G) is not quantitatively exact. The input zone was in the region  . Units on the
. Units on the  -axis are
-axis are  in all panels.
in all panels.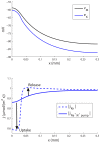
 ) was more negative than
) was more negative than  at all points along the
at all points along the  -axis. The Kir-channel thus exclusively mediated an outward K+-current. (B) In the input zone
-axis. The Kir-channel thus exclusively mediated an outward K+-current. (B) In the input zone  was close to
was close to  , and the outward Kir-current was small compared to the inward current through the Na+/K+-pump. In the decay zone, the outward Kir-current was bigger, and dominated over the inward current through the Na+/K+-pump. Therefore, the astrocyte took up up K+ in the input zone, and released K+ in the decay zone (as indicated by arrows in (B)).
, and the outward Kir-current was small compared to the inward current through the Na+/K+-pump. In the decay zone, the outward Kir-current was bigger, and dominated over the inward current through the Na+/K+-pump. Therefore, the astrocyte took up up K+ in the input zone, and released K+ in the decay zone (as indicated by arrows in (B)).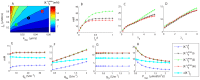
 (maximal extracellular
(maximal extracellular  in the input zone) to variation in selected model parameters. (A) Sensitivity to input flux density (
in the input zone) to variation in selected model parameters. (A) Sensitivity to input flux density ( ) and the output rate constant (
) and the output rate constant ( ). Similar values of
). Similar values of  were obtained for the three marked data points: (i) black:
were obtained for the three marked data points: (i) black:  ,
,  (default conditions), (ii) green:
(default conditions), (ii) green:  ,
,  , and (iii) red:
, and (iii) red:  ,
,  . B–D) Sensitivity to the length of the input zone (
. B–D) Sensitivity to the length of the input zone ( ), and tortuosities in the ECS (
), and tortuosities in the ECS ( ) and ICS (
) and ICS ( ). (E–H) Sensitivity of
). (E–H) Sensitivity of  and
and  (baseline extracellular
(baseline extracellular  ) to membrane conductances (
) to membrane conductances ( ,
,  and
and  ), and the maximal Na+/K+-pump rate (
), and the maximal Na+/K+-pump rate ( ).
).  . (B–H) The legend applies to all panels. Black (i), red (ii) and green (iii) lines correspond to the input-parameter combinations marked in (A).
. (B–H) The legend applies to all panels. Black (i), red (ii) and green (iii) lines correspond to the input-parameter combinations marked in (A).
 ). In two versions (blue lines), the original ECS volume fraction (
). In two versions (blue lines), the original ECS volume fraction ( ) was kept when the astrocyte was removed. (B) The performance of the six model versions were compared in terms of maximal
) was kept when the astrocyte was removed. (B) The performance of the six model versions were compared in terms of maximal  in the input zone during a constant K+ influx to the system. (C) To compare the time course of the
in the input zone during a constant K+ influx to the system. (C) To compare the time course of the  dynamics, the responses (in B) were normalized to the peak amplitude for each respective trace.
dynamics, the responses (in B) were normalized to the peak amplitude for each respective trace.Similar articles
-
Mechanisms of astrocytic K(+) clearance and swelling under high extracellular K(+) concentrations.J Physiol Sci. 2016 Mar;66(2):127-42. doi: 10.1007/s12576-015-0404-5. Epub 2015 Oct 27. J Physiol Sci. 2016. PMID: 26507417 Free PMC article.
-
Astrocytic mechanisms explaining neural-activity-induced shrinkage of extraneuronal space.PLoS Comput Biol. 2009 Jan;5(1):e1000272. doi: 10.1371/journal.pcbi.1000272. Epub 2009 Jan 23. PLoS Comput Biol. 2009. PMID: 19165313 Free PMC article.
-
Activity-dependent astrocyte swelling is mediated by pH-regulating mechanisms.Glia. 2017 Oct;65(10):1668-1681. doi: 10.1002/glia.23187. Epub 2017 Jul 26. Glia. 2017. PMID: 28744903
-
Role of the Astrocytic Na(+), K(+)-ATPase in K(+) Homeostasis in Brain: K(+) Uptake, Signaling Pathways and Substrate Utilization.Neurochem Res. 2015 Dec;40(12):2505-16. doi: 10.1007/s11064-014-1505-x. Epub 2015 Jan 3. Neurochem Res. 2015. PMID: 25555706 Review.
-
Ionic changes and alterations in the size of the extracellular space during epileptic activity.Adv Neurol. 1986;44:619-39. Adv Neurol. 1986. PMID: 3518349 Review.
Cited by
-
Changes in Astroglial K+ upon Brief Periods of Energy Deprivation in the Mouse Neocortex.Int J Mol Sci. 2022 Apr 27;23(9):4836. doi: 10.3390/ijms23094836. Int J Mol Sci. 2022. PMID: 35563238 Free PMC article.
-
Investigate channel rectifications and neural dynamics by an electrodiffusive Gauss-Nernst-Planck approach.PLoS Comput Biol. 2025 Jun 30;21(6):e1012883. doi: 10.1371/journal.pcbi.1012883. eCollection 2025 Jun. PLoS Comput Biol. 2025. PMID: 40587520 Free PMC article.
-
Cerebrospinal Fluid Flow.Annu Rev Fluid Mech. 2023;55:237-264. doi: 10.1146/annurev-fluid-120720-011638. Epub 2022 Sep 28. Annu Rev Fluid Mech. 2023. PMID: 39691763 Free PMC article.
-
Potassium and sodium microdomains in thin astroglial processes: A computational model study.PLoS Comput Biol. 2018 May 18;14(5):e1006151. doi: 10.1371/journal.pcbi.1006151. eCollection 2018 May. PLoS Comput Biol. 2018. PMID: 29775457 Free PMC article.
-
An electrodiffusive neuron-extracellular-glia model for exploring the genesis of slow potentials in the brain.PLoS Comput Biol. 2021 Jul 16;17(7):e1008143. doi: 10.1371/journal.pcbi.1008143. eCollection 2021 Jul. PLoS Comput Biol. 2021. PMID: 34270543 Free PMC article.
References
-
- Hansson E, Rönnbäck L (2003) Glial neuronal signaling in the central nervous system. FASEB journal: official publication of the Federation of American Societies for Experimental Biology 17: 341–8. - PubMed
-
- Zagami C, O'shea R, Lau C (2005) Regulation of glutamate transporters in astrocytes: evidence for a relationship between transporter expression and astrocytic phenotype. Neurotoxicity 7: 143–149. - PubMed
-
- Simard M, Nedergaard M (2004) The neurobiology of glia in the context of water and ion homeostasis. Neuroscience 129: 877–96. - PubMed
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources
Other Literature Sources
Medical
Molecular Biology Databases

