Methods for recording and measuring tonic GABAA receptor-mediated inhibition
- PMID: 24367296
- PMCID: PMC3852068
- DOI: 10.3389/fncir.2013.00193
Methods for recording and measuring tonic GABAA receptor-mediated inhibition
Abstract
Tonic inhibitory conductances mediated by GABAA receptors have now been identified and characterized in many different brain regions. Most experimental studies of tonic GABAergic inhibition have been carried out using acute brain slice preparations but tonic currents have been recorded under a variety of different conditions. This diversity of recording conditions is likely to impact upon many of the factors responsible for controlling tonic inhibition and can make comparison between different studies difficult. In this review, we will firstly consider how various experimental conditions, including age of animal, recording temperature and solution composition, are likely to influence tonic GABAA conductances. We will then consider some technical considerations related to how the tonic conductance is measured and subsequently analyzed, including how the use of current noise may provide a complementary and reliable method for quantifying changes in tonic current.
Keywords: GABAA; extrasynaptic; methods; noise; tonic inhibition.
Figures
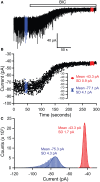
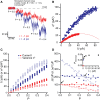
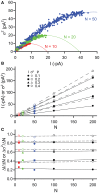
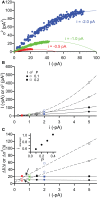
References
-
- Abramian A. M., Comenencia-Ortiz E., Vithlani M., Tretter E. V., Sieghart W., Davies P. A., et al. (2010). Protein kinase C phosphorylation regulates membrane insertion of GABAA receptor subtypes that mediate tonic inhibition. J. Biol. Chem. 285, 41795–41805 10.1074/jbc.M110.149229 - DOI - PMC - PubMed
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

