How does symmetry impact the flexibility of proteins?

Abstract

It is well known that (i) the flexibility and rigidity of proteins are central to their function, (ii) a number of oligomers with several copies of individual protein chains assemble with symmetry in the native state and (iii) added symmetry sometimes leads to added flexibility in structures. We observe that the most common symmetry classes of protein oligomers are also the symmetry classes that lead to increased flexibility in certain three-dimensional structures-and investigate the possible significance of this coincidence. This builds on the well-developed theory of generic rigidity of body-bar frameworks, which permits an analysis of the rigidity and flexibility of molecular structures such as proteins via fast combinatorial algorithms. In particular, we outline some very simple counting rules and possible algorithmic extensions that allow us to predict continuous symmetry-preserving motions in body-bar frameworks that possess non-trivial point-group symmetry. For simplicity, we focus on dimers, which typically assemble with twofold rotational axes, and often have allosteric function that requires motions to link distant sites on the two protein chains.

Keywords: allostery; flexibility; pebble game algorithms; proteins; rigidity of frameworks; symmetry.

Figure 1.

Proteins with , and symmetry. (a) The dimer tryptophan repressor—shown in cartoon representation—has symmetry, where the two colours represent the two chains. (b) Bacterial l-lactate dehydrogenase (PDB ID: 1lth) has symmetry. (c) N-phosphonacetyl-l-aspartate (PDB ID: 8atc)—shown in surface representation—has symmetry, where colours distinguish separate chains. This complex is formed with two types of chains, six copies of each, which corresponds to the 6 + 6 notation for this family of proteins in table 1. Each colour contains two dimers with two different chains in each dimer (i.e. in each colour, one dimer is built of chains A and C, and the other dimer is built of chains B and D). These structures were generated with Pymol (http://pymol.sourceforge.net). (Online version in colour.)

Figure 2.

Tryptophan repressor with (a) no tryptophan bound (PDB ID: 3wrp), (b) one tryptophan bound and (c) both tryptophans bound (PDB ID: 1wrp). Both (a) and (c) have symmetry, and it is speculated that symmetry is preserved in (b), as has been observed for symmetric allosteric proteins such as arginine repressor [24]. (Online version in colour.)

Figure 3.

(a) A body–bar framework, (b) a body–hinge framework and (c) a molecular framework. (Online version in colour.)

Figure 4.

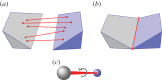
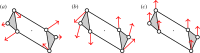
An example of a body–bar framework (G,q) with point group , shown looking down the axis. (a) The infinitesimal flex shown is -symmetric, since all the velocity vectors remain unchanged by the half-turn C₂. (b) The infinitesimal motion shown is a -symmetric trivial infinitesimal motion (corresponding to a rotation about the C₂ axis). (c) The trivial infinitesimal motion shown is not -symmetric, since the initial velocity vectors of the motion are reversed by C₂. (Online version in colour.)

Figure 5.

Two basic conformations of cyclohexane: (a) the ‘boat’ has half-turn symmetry and is flexible; (b) the ‘chair’ has threefold rotational symmetry and is rigid.

Figure 6.

An eightfold molecular ring realized with symmetry. Larger and smaller spheres indicate atoms that lie respectively in front of and behind the median plane of the structure.

Figure 7.

(a) A flexible structure that satisfies the orbit counts of theorem 5.1, but violates Tay’s non-symmetric counts. The structure consists of two fourfold molecular rings (placed horizontally), which are connected by four single bars. (b) The vectors indicate an antisymmetric infinitesimal flex of the structure. (Online version in colour.)

Figure 8.

Three samples for the runs of algorithm 7.2. See also [35] for a detailed demonstration of the symmetric pebble game. (a) The algorithm declares the edges r and r′ to be in R₁ in the first step, if tested last in the run on . It accepts all other edges not crossing ℓ in and all bridging edges (crossing ℓ) in E₂. So, in step (1), the algorithm predicts no non-trivial motion since |E₁∪E*₁∪E₂|= 6+6+6=18=6|B|−6. In step (2), the algorithm predicts a non-trivial symmetric motion since |E₁∪E₃|=6+3=9<10=6|B₀|−2. (b) The algorithm (applied to the same graph as in (a), but with a different choice of representatives for the vertex orbits) accepts all edges not crossing the new line ℓ in . All bridging edges except r and r′ are placed in E₂, while r and r′ (tested last among bridging pairs) are placed in R₁. So the counts are |E₁∪E*₁∪E₂|=3+3+12=18=6|B|−6 (again predicting no non-trivial motion in step (1)) and |E₁∪E₃|=3+6=9<10=6|B₀|−2 (again predicting symmetric flexibility in step (2)). (c) All edges not crossing ℓ are placed in , all bridging edges except q and q′ are placed in E₂, and q and q′ are placed in Q. Therefore, in step (1) of the algorithm we obtain |E₁∪E*₁∪E₂|= 3+3+12=18=6|B|−6, and in step (2) we obtain |E₁∪E₃|=3+7=10=6|B₀|−2, and hence no non-trivial motion is detected. (Online version in colour.)

Figure 9.

(a) The underlying multigraph G of cyclohexane, where each edge represents an implicit package of five edges. (b) The -symmetric ‘orbit graph’ G₀ of cyclohexane. (c,d) The graph and its symmetric copy . (Online version in colour.)

Figure 10.

A tomato bushy stunt virus (PDB ID: 2tbv) with icosahedral symmetry. (Online version in colour.)