A simulation of cross-country skiing on varying terrain by using a mathematical power balance model
- PMID: 24379718
- PMCID: PMC3872006
- DOI: 10.2147/OAJSM.S39843
A simulation of cross-country skiing on varying terrain by using a mathematical power balance model
Abstract
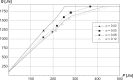
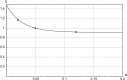
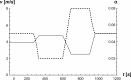
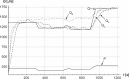
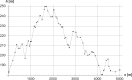
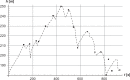
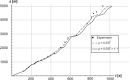
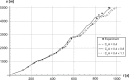
The current study simulated cross-country skiing on varying terrain by using a power balance model. By applying the hypothetical inductive deductive method, we compared the simulated position along the track with actual skiing on snow, and calculated the theoretical effect of friction and air drag on skiing performance. As input values in the model, air drag and friction were estimated from the literature, whereas the model included relationships between heart rate, metabolic rate, and work rate based on the treadmill roller-ski testing of an elite cross-country skier. We verified this procedure by testing four models of metabolic rate against experimental data on the treadmill. The experimental data corresponded well with the simulations, with the best fit when work rate was increased on uphill and decreased on downhill terrain. The simulations predicted that skiing time increases by 3%-4% when either friction or air drag increases by 10%. In conclusion, the power balance model was found to be a useful tool for predicting how various factors influence racing performance in cross-country skiing.
Keywords: air drag; friction coefficient; metabolic rate; power balance; skiing; work rate.
Figures
References
-
- Saltin B. The physiology of competitive c.c. skiing across a four decade perspective; with a note on training induced adaptations and role of training at medium altitude. In: Müller E, Schwameder H, Kornexl E, Raschner C, editors. Science and Skiing. London, UK: E and FN Spon; 1997. pp. 435–469.
-
- Smith GA. Biomechanical analysis of cross-country skiing techniques. Med Sci Sports Exerc. 1992;24(9):1015–1022. - PubMed
-
- Bergh U, Forsberg A. Influence of body mass on cross-country ski racing performance. Med Sci Sports Exerc. 1992;24(9):1033–1039. - PubMed
-
- Norman RW, Komi PV. Mechanical energetics of world-class cross-country skiing. J Appl Biomech. 1987;3:353–369.
-
- Holmberg HC, Rosdahl H, Svedenhag J. Lung function, arterial saturation and oxygen uptake in elite cross country skiers: influence of exercise mode. Scand J Med Sci Sports. 2007;17(4):437–444. - PubMed
LinkOut - more resources
Full Text Sources
Other Literature Sources
Research Materials

