Population decoding in rat barrel cortex: optimizing the linear readout of correlated population responses

Abstract

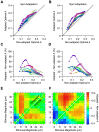
Sensory information is encoded in the response of neuronal populations. How might this information be decoded by downstream neurons? Here we analyzed the responses of simultaneously recorded barrel cortex neurons to sinusoidal vibrations of varying amplitudes preceded by three adapting stimuli of 0, 6 and 12 µm in amplitude. Using the framework of signal detection theory, we quantified the performance of a linear decoder which sums the responses of neurons after applying an optimum set of weights. Optimum weights were found by the analytical solution that maximized the average signal-to-noise ratio based on Fisher linear discriminant analysis. This provided a biologically plausible decoder that took into account the neuronal variability, covariability, and signal correlations. The optimal decoder achieved consistent improvement in discrimination performance over simple pooling. Decorrelating neuronal responses by trial shuffling revealed that, unlike pooling, the performance of the optimal decoder was minimally affected by noise correlation. In the non-adapted state, noise correlation enhanced the performance of the optimal decoder for some populations. Under adaptation, however, noise correlation always degraded the performance of the optimal decoder. Nonetheless, sensory adaptation improved the performance of the optimal decoder mainly by increasing signal correlation more than noise correlation. Adaptation induced little systematic change in the relative direction of signal and noise. Thus, a decoder which was optimized under the non-adapted state generalized well across states of adaptation.

Figure 1. Population decoding.

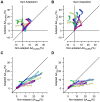
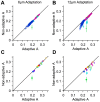
A. Schematic representation of linear combination of neuronal activity by the downstream decoder. Coefficients , and represent the synaptic weights between the neurons (top row circles) and the decoder (bottom). B. Schematic representation of pooling (left panel) and optimal decoding (right panel). The green and blue ovals represent the joint distribution of the neurons' responses to two sensory stimuli. The solid black line represents the weight vector. The pooling method (left panel) is equivalent to a weight vector along the identity line. The bell-shaped areas on the weight vector represent the projection of the neuronal response distribution for each stimulus. Dashed lines correspond to the best criterion to discriminate the two stimuli. The insets show the hit rate versus false alarm rate (ROC) for every possible criterion, shading indicates area A. C. Average value of A for the pooled neuronal responses plotted against the average value of A for the best neuron. Various population sizes within a session are plotted with the same color and connected with a line. For each population size, the value of A is averaged across all possible selections of that size. D. The average value of A, for each stimulus pair, under pooling (upper triangle) and optimal decoding (lower triangle), across all populations of 8 single neurons. E. Histogram of the optimal weights as a function of the signal-to-noise ratio of the same neuronal populations as in D. The weights and SNR values are normalized to the best neuron in each population.

Figure 2. Pairwise- and groupwise-optimal decoding schemes.

A. Schematic representation of pairwise- and groupwise-optimal decoding. B. The average value of A for a range of population sizes. Data from neuronal populations within a session are plotted with the same color and connected with a line. Filled markers correspond to populations of single units. For each population size of single units, the value of A of all possible selections of that size was averaged within session. Open markers correspond to further additions of multi-units to the whole population of single units. Thus the direction of increasing population size is from filled markers to open markers. For every population of mixed single and multi-units, the value of A was obtained by averaging across a maximum of 400 possible selections within a session. C. as in B, but for groupwise-optimal decoding.

Figure 3. Decoder tolerance to weight vector deviation.

A. The relative decline in the performance of the decoder after dropping a unit by setting its weight to zero. For every population, the performances were calculated and averaged across all possible 1-unit reductions. Plotting conventions are the same as in Figure 2. B. The performance of the decoder after dropping a unit relative to the performance of the pooling of the reduced population. The abscissa represents the size of the population after 1-unit reduction. C. Rotating the weights from the optimal direction towards the identity line which corresponds to pooling. Rotation was performed along two asymmetric paths. D. The relative change in the performance of the decoder when the weight vector was deviated from the optimal direction in steps of 10° towards the pooling direction (identity line). Every session is represented with a color and corresponding data points are connected with a line. The two extreme data points on each curve correspond to the performance of pooling relative to the groupwise-optimal decoder. For every session, the population of all single neurons was considered. E. 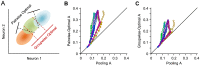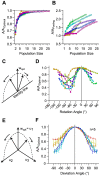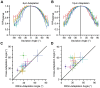Systematically rotating the weights from the optimal direction, denoted by , towards every other dimension in the space of neuronal activities. Dimensions are orthogonal, and span the space of the neuronal activity. The trajectory of this rotation lies on the 2-dimensional plane spanned by the optimal direction and the target dimension, and hence is perpendicular to all other dimensions. F. The relative performance of decoder with a deviated weight vector compared to the optimal direction for all possible populations of 8 neurons averaged across sessions (n = 5). Colors indicate the 7 trajectories toward associated dimensions, with red corresponding to the dimension perpendicular to optimal direction such that it maximizes the separation between neuronal responses, and blue corresponding to the dimension along which the separation between neuronal responses is minimal. Error bars indicate standard error of the means.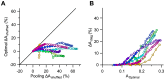

Figure 4. Effect of noise correlation on decoding.

A. The ordinate represents the relative effect of noise correlation. This is captured by the per cent change in the value of A for a groupwise decoder optimized on trial-shuffled neuronal responses. The abscissa indicates the effect of noise correlation on pooling scheme. This is captured by the increase in the value of A for pooling after trial-shuffling neuronal responses. Color conventions and selection of neurons for every population are identical to Figure 2. For every selection of neurons for a given population size, the values of A for 50 trial-shuffles were averaged. B. The effect of ignoring noise correlation when decoding. ΔA_diag corresponds to the per cent drop in the performance of a decoder which ignores noise correlation. Noise correlations were ignored by setting the off-diagonal elements of the total covariance matrix to zero.

Figure 5. Adaptive optimal decoding.

A. The value of A for the optimal decoder when optimized on population responses under 6 µm adaptation, against the value of A for the optimal decoder when optimized on non-adapted population responses. B. As in A, but for 12 µm adaptation. C. The per cent improvement in the value of A under 6 µm adaptation relative to the non-adapted state. D. As in C, but for 12 µm adaptation. E. The effect of 6 µm adaptation on the value of A for every stimulus pair, in a sample session with 11 simultaneously recorded single neurons, indicated by purple color in A–D. The upper triangle corresponds to the groupwise-optimal decoder, while the lower triangle corresponds to the pairwise-optimal decoder. F. As in E, but for 12 µm adaptation.

Figure 6. Effect of noise correlation on the adaptive optimal decoder.

A. The per cent change in the value of A by trial-shuffling, denoted by ΔA_shuffled, for 6 µm adaptation, against the same measure in the non-adapted state. B. As in A, but for 12 µm adaptation. C. The per cent drop in the value of A by ignoring noise correlation when decoding, denoted by ΔA_diag, for 6 µm adaptation, against the same measure in the non-adapted state. D. As in C, but for 12 µm adaptation.

Figure 7. Effect of adaptation on signal correlation.

A. The eigenvalues of the signal correlation matrix for populations of 8 simultaneously recorded neurons, sorted into descending order. Each eigenvalue was normalized to the sum of all eigenvalues. Error bars indicate standard error of the means across sessions (n = 5). The colors red, green and blue correspond to the non-adapted state, 6 µm adaptation and 12 µm adaptation, respectively. The right panel illustrates the normalized eigenvalues for stimulus-shuffled neuronal responses. The stimulus labels for each neuron in a given population were randomly shuffled 100 times, and the corresponding eigenvalues were averaged. B. Signal correlation as captured by the signal correlation index as a function of population size under the three adaptation states. For population sizes 72 and 73, all possible selections of neurons (n = 73 and 1, respectively) and for the other population sizes 500 random selections of neurons were used to obtain the signal correlation index. Color convention is identical to B. C. The performance ratio of groupwise-optimal decoder to pairwise optimal decoder as a function of signal correlation index for the populations in B. Different population sizes are plotted in different levels of brightness with the colors red, green and blue corresponding to the non-adapted state, 6 µm adaptation and 12 µm adaptation, respectively. Each data point corresponds to one population. The inset shows the distribution of correlation coefficients calculated per population size for each adaptation state.

Figure 8. Performance of various coding schemes under different states of adaptation.

A. The discrimination performance of the pairwise-optimal decoder (solid thick black curve), the groupwise-optimal decoder (solid thin black curve) and pooling (gray line) in the non-adapted state, as a function of population size. For every population size the value of A was averaged across 500 random selections of single neurons from all recorded single neurons (n = 73). For population sizes 1, 72 and 73 the possible distinct selections from 73 single neurons were 73, 73 and 1, respectively. Thus for these population sizes the value of A was averaged across all possible selections. B. As in A, but for the 6 µm adaptation. The inset represents the relative change in the average value of A through sensory adaptation. C. As in B, but for 12 µm adaptation.

Figure 9. Decoding generalization across adaptation states.

A. The abscissa indicates the value of A for the optimal decoder when optimized on half of the adapted responses and tested on the other half for 6 µm adaptation across populations of 8 single neurons. The ordinate corresponds to the value of A for the optimal decoder when optimized on half of the non-adapted responses and tested on the same half of the adapted responses as in the abscissa. Error bars indicate standard error of the means. Colors indicate different sessions. B. As in A, but for 12 µm adaptation. C. As in A, but for whole session populations. Filled markers represent populations comprising single units only, while open markers indicate the whole set of simultaneously recorded single- and multi-units in a session. D. As in C, but for 12 µm adaptation.

Figure 10. Adaptive and non-adaptive decoding tolerance to weight vector deviation.

A. The relative performance of adaptive decoding with a deviated weight vector compared to the optimal direction for all possible populations of 8 neurons averaged across sessions (n = 5) for 6 µm adaptation state. Colors indicate the 7 trajectories toward associated dimensions, with red corresponding to the dimension perpendicular to optimal direction such that it maximizes the separation between neuronal responses, and blue corresponding to the dimension along which the separation between neuronal responses is minimal. Error bars indicate standard error of the means. B. As in A, but for 12 µm adaptation. C. Abscissa represents the angular difference of optimal weight vectors for non-overlapping trial-halves within the 6 µm adaptation state. Ordinate represents the angular difference for 6 µm adaptation versus non-adapted state. For each session, the angular differences were averaged across 100 times of random trial-halving. Error bars indicate standard error of the means. Colors indicate different sessions. D. As in C, but for 12 µm adaptation.